Remember those Sec One days? The days when you walked into school with a stupid-looking water bottle slung across your chest and, for the boys, when the hair was just starting to grow on your legs (please don’t think sideways. tsk.).
Sadly, many students studying for their final exams tend to get so caught-up with major NC-16 topics like Transformations and Vectors that they’ve forgotten about these good o’ pre-pubescent days.
So when they see something like this in the exam,
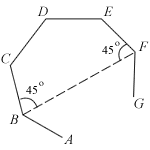 ABCDEFG is part of a regular n-sided polygon. Given that ∠CBF = ∠EFB = 45o, find n.
ABCDEFG is part of a regular n-sided polygon. Given that ∠CBF = ∠EFB = 45o, find n.
… they end up scrutinizing the diagram (if there’s one) for long periods, wondering if it had been drawn correctly.
Now given that a question on polygons will almost always appear somewhere in your Paper 1, Miss Loi shall help refresh your post-puberty memory by pulling this straight out from the cartoon-laden pages of your Sec One textbook:
Sum of interior angles in a n-sided polygon = (n-2)180o
Can already hear all the “Chezzzz … so simple!“.
Welcome to the egoistic world of adulthood.


 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 





















13 Comments
曜
日
haha i couldn't answer it
damn i feel stupid
曜
日
Hey encik, you're supposed to be an ultra U-Grade joss sticks burner!
曜
日
eh is this a synergy of simultaneous equations and geometry? if i do simultaneous this way..
let angle EBA be a
(180 - 45 - a) divide by 360 = n
135 - a = 360n
135 - 360n =a (equation 1)
[(n-2) 180] / n = 45+ a (equation 2)
sub equation 1 into 2 and
(180n - 360)n = 45 + 135 - 360n
180n - 360 = 180n - 360 (n^2)
but however after equating i get n^2 = 1
wad de-.-""?
曜
日
actually is the equation (180 - 45 - a) / 360 = n wrong? somehow i used another polygon the numbers were wrong but if i recall it should be 180 - interior then divided by 360 = number of sides
曜
日
oh nono it should be exterior angle divded by 360..got confused..
曜
日
wow this is one insane q i cant solve brain isnt working..zz nvm slp time will try tmr =x
曜
日
hi, can AB be parallel to EF?
曜
日
Welcome to Jφss Sticks 123!
Errr ... one reason for putting up this question is to show students that sometimes a diagram can be more bane than boon!
In this case you shouldn't be scrutinizing the finer points of the diagram - you will get more confused the longer you stare at it!
Focus on the given formula instead!
曜
日
To answer kiroii's comment on another post, the question says it's a polygon with n. How are you going to draw a such a polygon? So do you even think that the diagram above is accurate?
BUT even though the diagram can't accurately depict an n-sided polygon, it does a fine job of depicting another polygon with a finite number of sides.
Get the drift?
曜
日
nop i still dunget it >.< anyway miss loi uh i was wondering are you free to conduct a tution class to teach me relative velocity? in 1 lesson and what are ur rates
曜
日
Check your inbox dude. Already replied you on Thursday.
曜
日
Hi ms loi can u help me view my solution??
http://img509.imageshack.us/img509/6047/solutionks5.jpg
曜
日
Awww 123` Miss Loi is so touched by you putting up your workings.
And yes n = 12 so expect to find some confetti on your head soon!
But Miss Loi prefers to do it this way:
As described, the diagram is highly inaccurate BUT for sure you'll see a 5-sided polygon (even though it's irregular). This will be the ONLY time Miss Loi uses the diagram.
Now by substituting n = 5 into the formula, you'll get:
45o + 45o + 3x = (5-2)180o
where x is each of the unknown interior angle of the polygon.
Solving for this you'll get x = 150o.
Next, if each interior angle of this n-sided polygon is 150o, then the sum of all the interior angles will be 150o*n. So we can derive the final equation:
150o*n = (n-2)180o
If you solve this you'll get n =12 too!
Well to each his/her own. But in this case, Miss Loi personally prefers the reliability of equations than to make potentially risky assumptions on inaccurate diagrams.
But well done and thanks for solving this pre-pubescent question!