To aid those who have run out of questions to do (your kind actually exist???), and as a form of (ahem) public service for the cause against the LMBFH Syndrome, Miss Loi will post here from time to time questions that she found (either during her daily tuition or by her own creation) to be challenging, interesting, important, introspective, deep, meditative , sadistic (haha) etc. etc…
Enough of lame intros, let’s kick-off with the first question!
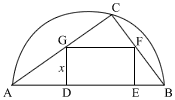
A semi-circle is shown with diameter AB. Rectangle DEFG is drawn within triangle ABC. Given that AC = 8 cm and BC = 6 cm, find
- The perpendicular distance from C to AB.
- Let DG be x. Show that the area of rectangle DEFG, A m2, is given by
A = 10x – (25/12)x2 - What’s the value of x for A to have a stationary value? Is this value of A a maximum or a minimum?
Answers on a post card please 🙂
頑張って!!!
8 Comments
曜
日
1) h=4.25
the rest dunno so difficult maybe too tired ...
曜
日
EEW! EEW! EEEEEEEWWW!!!
曜
日
As a geometry teacher, I like this problem. It touches on properties of semicircles, area of triangles, coordinate geometry, and a little derivative at the end. Oh yes, and the height is NOT 4.25 (I don't want to spoil the answer, but it's a little taller).
曜
日
Wah Level 10 guru here to comment! *Kneels down and bow*
John: someone's trying to pwn u!
I should put the answers up soon but some of my students still haven't try yet - slackers! (Just joking here la - actually they're also very busy with school at the moment :))
曜
日
haha... i got h=4.8cm, the rest dunno how to do. =P
曜
日
Ok answer time *drum roll*!
Part 1:
AB = √(82 + 62) = 10 cm
∴ Area of ABC = (1/2)(8)(6) = 24 cm2
h being height of triangle ABC, so solving this equation:
(1/2)(h)(AB) = 24 cm2
You should get h = 4.8 cm! 🙂 (shihui where u want Miss Loi to treat u???)
Part 2:
Using similar triangles,
(GF)/(AB) = (h-GD)/h
GF = AB(1 - GD/h)
= (10)(1 - x/h)
= 10 - 10x/h
Now using the value of h from part 1, 10/h = 10/4.8 = 25/12.
GF = 10 - (25/12)x
∴ A = GD x GF
= x( 10 - (25/12)x )
= 10x - (25/12)x2 🙂
Part 3:
∴ A is max when x = 2.4 cm 🙂
Wah type until fingers also numb liao! Actually managed to get all these maths symbols out!
BTW thanks to all of you who tried and responded but why all only do part 1???? Next time don't 半途而废喔!
曜
日
Anyway, I find that one of the steps in part 2 is wrong.
GF/ AB = GD / h
instead, it should be
GF/ AB = (h - GD)/h
Other than that, I agree with you that this is a gd qn. In fact, there are a lot of concepts tested in this qn.
曜
日
Thanks so much TYS, for pointing out this typo all the way back from the pioneering days of this blog!
At the same time, Miss Loi has taken the liberty to 'enhance' the readability of the said working (just a little). She's feeling so noob now looking at her early posts 😛