 Apparently the last Functions question was quite a QED.
Apparently the last Functions question was quite a QED.
So on a dark overcast day, Miss Loi was looking around for something a little more challenging, when a clairvoyant voice suddenly boomed in her head:
Miss Loi! Thou shalt post that Functions question on thy blog!
Slightly startled, Miss Loi looked up to the skies in the direction of the voice, and traced it to a break in the clouds where rays of light emanated from.
“But that question has only been seen once in the autumn of 2002. Besides that’s a premium question where mortals seldom tread.” she answered meekly.
The Darth Vader-like voice retorted sharply:
That is why, my sexy young tutor, post it up thou must! For this is the final year for the existing functions syllabus, and the constellations have aligned. I fear the time is nigh for it to appear again!
So here’s the premium Functions question, courtesy of some orders from above, which will will lead to a marshmallow popping into your mouth if you can get it right on the first try at The Temple:
The function f(x) = x3 + ax + b is such that the equation f(x) = x has solutions x = 1 and x = 2.
- Find the values of a and b.
- With these values of a and b, determine whether the curve y = f(x) has any turning points and hence explain why the inverse function exists for x ≥ 2.
- Evaluate f-1(15).
Mama drama aside, this is meant to test your understanding of inverse functions. Questions like this one (especially part 2 here) will usually require you to memorize and regurgitate the following Golden Phrase at some point in your answer:
The inverse of function f exists if f is one-to-one
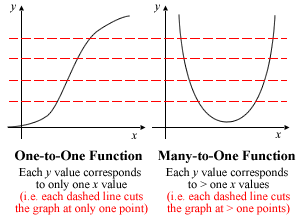
For those who have been confused by the non-human definitions of one-to-one and many-to-one functions in textbooks/notes till now, this diagram will hopefully help settle the issue once and for all:
For the premium part (i.e. part 3) of this question, note that f(x) is a cubic function, so you can’t use the usual let y = f(x) to find the inverse.
Instead it tests your understanding of this:
Domain of f-1 = range of f; range of f-1 = domain of f.
Actually it’s really quite simple once you know what to do. But Miss Loi better stop here as she has spoken too much already. 天机不可泄漏!
DISCLAIMER: Though the constellations may indicate otherwise, Miss Loi makes absolutely NO guarantee that the above question will appear in your upcoming O-Level exam. Moreover, the sky was nowhere near overcast today.



 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 





















20 Comments
曜
日
Waaaah... this post brings it all back to me. Those days of cracking my head over the maths equations are really truly over man!
曜
日
Walter, Miss Loi can certainly feel your utter, utter relief all the way from here!
曜
日
Wah!! This Maths problem can kill this lao Aunty. Leave it to the younger kids lah. hehe....
曜
日
Wa,,,,, this qn abit chim arh.... not the typical function that i normally practice....
Hm... still thinking
曜
日
Orh... actually quite simple la...
1)Subs x as 1 and 2 into the expression and equate them to x , (i.e.1 and 2). Then, Solve it by simultaneous eqn
a= -6 , b=6?
2)(Not sure) i use dy/dx then at stationary value, corresponding x is 2, ...i would use a sketched graph instead to prove that f(x) is one to one for >2 (can? :/)
3 equate x^3 -6x+6 = 15....solve it...x is 3 and -1.5
曜
日
a = (-7)
b = 6
f(x) = x^3 - 7x + 6
dy/dx = 3x^2 -7
thus x has 2 values which are -1.58 and 1.58
the coords of the turning are (1.58, -1.13) and
( -1.58, 1.13). thus the curve has 2 turning points..
but i dont see how is the 2nd part supposed to be done?
曜
日
as for the last question i got a feeling u gotta work back wards yet as i subed 15 as y i caant solve the cubic equation
曜
日
eh my first post got sent off to god knows where-.-
a= -7
b= 6
thus y = x^3 -7x +6
dy/dx = 3x^2 -7
thus with 2 coordinates there are turning points
曜
日
however i get the points at (1.58, -1.13)
and (-1.58, 1.13)
but with the y intercept being 6 and when x is 1 and 2 y = 0
the point (-1.58, 1.13) doesnt make sense thus i take it that it's to be rejected yet there is one turning point of the former
however the 2nd part i dun get it>.
曜
日
ECL, 现在是年轻人的世界了 ... sigh. But for the young & handsome people like kiroii and 123 and Jaymes, this should 'easy bitsy pom pi pi' haha.
曜
日
For part 1,
Young and handsome 123 has summarized the steps correctly. Miss Loi is stating the obvious here but sometimes students don't really catch the keywords has solutions, which means the x=1 or 2 to satisfy f(x) = x. Duh.
So simply sub in these values of x:
(1)3 + a(1) + b = 1
⇒ a + b = 0 ----- (1)
(2)3 + a(2) + b = 2
⇒ 2a + b = -6 ----- (2)
Sub a = -b from (1) into (2) to solve the simultaneous equations,
You'll get a = -6 and b = 6
So simple right? How did young and handsome kiroii get a = 7????
曜
日
For part 2, you don't have to waste precious time (especially during your exam) to find the exact coordinates or sketch out the curve itself.
You just have to show that you understand the following concept:
A one-to-one function cannot have any turning point. (see diagram above if you are not sure)
So since the question talks about x, first you'll have to find the value of x at the turning point(s), which kiroii and 123 rightly showed us the way:
df(x)/dx = 0
3x2 - 6 = 0
Solving the above,
x = ±√2
This means there are two turning points, one at x = √2 and another at x = -√2, which implies that f(x) is NOT one-to-one within this range.
But the question asks for x ≥ 2. Sadly this is where the insecure, under-confident, panic-stricken Singaporean student takes centrestage. (S)he will say "%#$*! The question says x = 2, how come I keep getting √2???!!", before proceeding redo and redo the question again.
Taking a page off that imaginary textbook called common sense, 2 is GREATER than √2 for goodness sake! Since the 2 turning points are contained within -√2 ≤ x ≤ √2, there will be no more turning points for x > √2 which also imply that there is no turning point for x ≥ 2!
So to answer this question in full, simply repeat the following. Everybody now!
The turning points of f(x) are found at x = ±√2. As f(x) has no turning points at x ≥ 2, it is a one-to-one function at x ≥ 2 and therefore f-1 exists.
Look ma, no diagrams required!
曜
日
For part 3,
As mentioned, once you know what to do it's pretty simple.
The range of f-1 = domain of f, and vice versa.
So y = f(x) maps to x = f-1(y)
From this you can simply let
f-1(15) = x
and you'll get:
15 = f(x) = x3 - 6x + 6
⇒ x3 - 6x -9 = 0
Classic textbook stuff, but unfortunately there will be stubborn students who are so intent on finding the full expression for f-1 first before doing anything else.
The tedious part, as Kiroii and 123 pointed out, is to solve this cubic equation where you'll need to do a bit of trial and error for your root (see your Factor Theorem chapter).
When you look at the constant of the cubic equation which is 9, the possible values of the root can only be ±1, ±3 and ± 9.
So let's see ... f(1) ≠ 0 ... f(-1) ≠ 0 ... f(3) = 0 (eureka!)
Factorizing the cubic function with (x -3) with your super-duper long division skills:
And you'll get:
(x - 3)(x2 + 3x + 3) = 0
To find the other roots from the quadratic equation, and using your
You'll discover that,
b2 - 4ac < 0
So there is only one solution for f-1(15) = 3
Yeah it's a little tedious but you do need to know all the possible roots of the cubic function in order to satisfy your final answer.
曜
日
The function f(x) = x3 + ax + b is such that the equation f(x) = x has solutions x = 1 and x = 2.
Find the values of a and b
err i was under de impression that "has solutions x=1 and x =2 " means that f(x) = 0 when x is 1 or 2 thus by equating them i got 7..
anyway de last part i did de samemethod but i couldnt solve due to my ans in de first part being incorrect..
曜
日
Patience kiroii,. It's always due to the spam filter thinking your comments were spammy with all those math symbols! Wait for Miss Loi to retrieve them from the spam box.
Read part 1 again. It says: The function f(x) = x3 + ax + b is such that the equation f(x) = x has solutions x = 1 and x = 2.
Don't always assume f(x) = 0!
P.S. Miss Loi have deleted your other two comments, since they are similar to your latest one.
曜
日
huh? then what ya mean by has solution x =1 and x =2 >.< i dun tink my teacher eleborated that before
ps:sry for spammin juz tat everytime i come bak i see my comments gone thus asummin it was a glich or some kind
曜
日
orh.....
hehe i used my calculator to solve the cubic equation.. thats why mayb got a wrong solution of 1.5
曜
日
kiroii,
Instead of using f(x) = 0, since this question specifically says f(x) = x, try thinking along the line of:
f(x) - x = 0 when x = 1, x = 2
Is it clearer now?
曜
日
123, lemme guess ... was it a Sharp calculator?
Let this be a reminder to you to show your workings properly during the exam. Calculators should only be used to confirm your answer.
BTW, if you didn't press wrongly, time to fix that calculator 🙂
曜
日
oh right i din scrutinised the q with sufficient prudence..