OK everyone, the following H2 9740 Maths Paper 1 suggested solutions (see below) that I’ve worked out are merely what it is i.e. suggested answers.
It is most certainly not the actual marking scheme from Cambridge, so don’t be quick to assume the end of the world for your Paper 1 should some of your steps and answers be different from mine. You’ve probably been told countless times that marks will still be awarded even though your answer may not be complete, as long as you have presented your concepts and ideas clearly 🙂
Of course, do kindly point out any mistake that you may spot in the solution. [disclaimer]Afterall, they were compiled rather quickly using whatever spare time I have left after my classes these two days.[/disclaimer]
Now that we’re halfway there, it’s time to focus on the following topics in your H2 Maths Paper 2 (while the H1 folks can forget about maths for a long, long time).
Pure Maths Topics
- Differential equations, integration by parts
- Applications of Differentiation (maxima & minima problems, connected rate of change, equations of tangent & normal)
- Vectors (foot of perpendicular distance, area of parallelograms/triangles etc.)
- Functions (composite functions, inverse functions, transformations)
- Inequalities
- Complex numbers (loci – hope you have your compass with you IF it comes out)
Statistics Topics
Though questions on statistics may appear to be quite random and unforeseeable at times, do spend time to look through the statistics portion of the 2007 and 2008 H2 Maths Paper 2 to have a feel of the section. It will be manageable as long as you are confident in your probability concepts. The importance of the 3 Cs in this section i.e. reading the questions/stories Calmly, Carefully and Correctly cannot be overemphasized. Make sure you iron out each question’s logic first instead of charging in like a mad man/woman!
- Probability (Venn diagram, probability tree, conditional probability, permutations & combinations)
- Methods & techniques of sampling (do spend bit of time reading it up)
- Poisson & binomial distributions (know the conditions for Normal approximations & perform continuity correction)
- Normal distribution (linear combinations of normal variables: sums and multiples)
- Linear regression (transforming a set of non-linear data to linear form, correlation coefficient r2=b∙d)
- Sampling & hypothesis testing (Central Limit Theorem, calculation of unbiased estimates of population mean & variance from a sample)
All the Very Best for Paper 2!!!


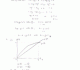


 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 





















28 Comments
曜
日
Perhaps we can consider Q4 as a question on transformation? (Refer to link above)
曜
日
mathsguidebook.com/h2maths/h2-maths-2009.php
曜
日
Yay most of my answers tally =D apart from the ones i mentioned earlier. Although i think i got 15 cm for the 13th bar in qn9... Aiyah lazy to go rework >_<... Thanks alot for the ans can go do paper 2 happily =D
曜
日
Congratulations! For question 9, a quick way to do this question is to observe that 13 is exactly halfway between 1 and 25. Take geometric mean of 1 and 25, answer is 10.
曜
日
Just to add, when drawing the perpendicular bisector for question 9, the perpendicular bisector does not just passes through the origin, it passes through according to the solution diagram.
according to the solution diagram.
曜
日
Hey! Is it possible to add H1's solution as well for this year? Thanks much! (:
曜
日
Eh Kohes, the question said that it DOES pass through the origin, and if u happen to use a protractor to draw (i had spare time to measure =P) i will pass though both the 7th root and origin.
Today's paper was average, For question 6 the world record timing should be 3mins 41.4 seconds right? And the family of solution curves were they point of inflextions? I used like C=20 and -20 before i could differentiate between the 3 graphs =X they are like on top of one another =X(for my case anyways)
曜
日
10(iii) Another method : Since (0,1,0) from line l and (2,3,4) lie on the plane P3. We will have 2 directional vectors (1,1,-1) and (2,2,4) to define the plane. Crossing these 2 vectors = (6,-6,0). So the vector eqn for the plane is r.(6,-6,0)=-6. Hence the cartesian eqn is z=0 and (x-y) = -1 !!!!
曜
日
Yeah, Nash that was what I was referring to. The diagram in the suggested solutions did not cut the 7th root though.
曜
日
Hey, I'm just wondering whether the cartesian equation given to question 10(iii) is correct. Shouldn't it be x - y + 0z = -1, or alternatively, x - y = -1, z can be any real number?
曜
日
hi when will p2 answers be posted up?? eager to find out answers!!!
曜
日
@passerby: p2 answers are out at mathsguidebook.com
曜
日
Thanks for the link kohes, are u a teacher or something O_o? Anyways the last part of Qn 11 is misleading, i thought probability of 0 and 1 is 0.2... tallied the results... ~70 for both papers =D
曜
日
Yeah, its the phrasing, some people interpreted it as P(R=0) or P(R=1). 🙂
Haha, I'm not a teacher of course. Just happen to be interested in such discussions, maths keeps my brain working!
曜
日
hey i was just wondering, how does the grading system work is it >70 for an A or does it fluctuate according to how everyone does?
曜
日
Hey will the chem 2009 h2 p3 and be out too?
曜
日
Well for the grading system u can refer to my earlier post on one of miss loi's Sec 4's posts...
https://www.exampaper.com.sg/blog/miss-loi-the-tutor/gce-o-level-octnov-2009-e-maths-4016-paper-2-suggested-answers-solutions
Its the same system for JC more or less and 70 is still a B =X... For maths the grade for A hovers around 80
曜
日
hello! i'm eagerly waiting for chem 2009 h2 p3 as well, cos i take h1 chem and i want to see if cambridge's style has perhaps changed for this year? (for last year it was organic spammage i heard)
曜
日
Yes it was an organic spam, every question had it cambridge dosnt like to repeat trends. Just in case u wanna know, P3 had 2 organic question, chem kinetics, protein chem ,grp7. Like i spotted they are gonna put transition for paper 2 and kill alot of ppl like the Cu chem question last year (ugh) Probably Mn or Vanadium this time(might come out as electro though)
I don't think Little miss Loi covers JC chem so maybe u should try other websites. Its already out according to my tutor but i dun have the links >_< sorry...
Omg i rank highest in the chatter boxers <_<, just noticed... Well its constructive conv anyways (mostly) =P
曜
日
Ikes true, JC chem doesn't seem to be covered here. i tried and tried Google using various search terms, but I guess I'll try again tomorrow, when whichever website hosting it gets indexed by Google. thanks for your info! :DD
曜
日
Oh ok thanks! Do you all mind putting the link here once you all find it? Thanks a million! (: wad ques did you all do for chem?
曜
日
Sorry guys I've been away for the past week as I was busy with my classes and working out the solutions to the rest of the H1/H2 maths papers.
Anyway for those of you who are not yet aware, my H1 Maths Paper 1 and H2 Maths Paper 2 are now up.
I appreciate your discussions and comments here, and in response to some of the feedback, I've updated the diagrams in Q9 to more show more accurately that the bisector does indeed pass through the origin and z7.
曜
日
And to elaborate on Labbitan's method to get the cartesian equation of the plane (let's call it p4) in Q10(iii),
We let d1 be the direction vector of l i.e.
d1 =
We're given that (2, 3, 4) lies on p4, and since we've proven that l lies on p4
⇒ (0, 1, 0) lies on p4 too
⇒ we can form another direction vector d2 on the plane as follows:
d2 =
We can then cross d1 and d2 to obtain the normal of plane p4:
d1 × d2
=
So to get the cartesian equation of p4:
r⋅
∴ x − y = −1, z ∈ ℝ
(yes passerby it's z ∈ ℝ, I've updated the solution 😉 )
Lastly, I would like to add that we can also show that line l lies in p3 through the following two expressions:
x+z = 0 ⇒ x = −z
y+z = 1 ⇒ y = 1−z
that's obtained using the RREF function in your GC when solving the equations of p1 & p2 in part (ii).
We can then sub the above expressions into the equation for p3 as follows:
LHS: 2(−z)+(1−z)+3z−1+k(z+2(1−z)+z−2) = 0 = RHS
∴ l lies in p3 for any constant k.
曜
日
wah.. so late then it's out.... alrd finish a level liao....
曜
日
hi,
for qn7ii, you need to expand (a+bx^2)^(-1) one more time as (1+b/a x^2) ^2 will have a term in x^2.
曜
日
Hello there 'Cher.
Moved your comment here as I believe you're referring to the 2009 H2 Maths P1 and not the 2008 one.
Errr ... for the relevant part of Q7(ii), the binomial expansion of (a+bx2)−1 is as follows:


Since is the b in (1+b)n, the next term would contain a x4 if we were to 'expand one more time' as follows:
is the b in (1+b)n, the next term would contain a x4 if we were to 'expand one more time' as follows:
From the above we can see that there is no x2 beyond the second term. I suspect that you've taken instead to be your b in (1+b)n?
instead to be your b in (1+b)n?
stormangel: This blog post was published on 12 Nov 2009 (two days after your H2 Paper 1) - very late meh?
曜
日
hello
anyone knows where to find the ans to A level chem our year ?
曜
日
as in 2009. thanks especially to paper 1.