It has been a holy weekend with an unholy schedule for Miss Loi. As this hectic weekend (thankfully) comes to an end, Miss Loi would like to leave you with a question on Similarity. Miss Loi’s students will know that she has an unnatural fetish for these questions (triangles and all) as they sometimes tend to pop up uninvited and unannounced in Vectors area as well.
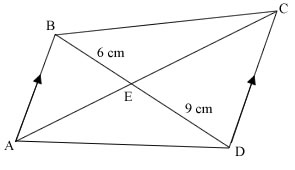
ABCD is a quadrilateral with AB parallel to DC. AC and BD meet at E where BE = 6 cm and DE = 9 cm.
- Given than AC = 35 cm, find the length of AE.
- Find the ratio of area of triangle BCE : area of triangle CDE.
- Find the ratio of area of triangle ABE : area of triangle CDE.
- Find the ratio of area of triangle BCE : area of triangle ADE.
Ok that’s all for now while Miss Loi takes a sip of coffee and enjoys the brilliant sunset in front of her, contrary to what is being reported in her Ever-Reliable Apple Weather Widget *sigh!*

 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 





















4 Comments
曜
日
1. A little diagram for clarity 🙂
In △ABE & △CDE,
∠ABE=∠CDE (alt ∠s, AB//CD)
∠EAB=∠ECD (alt ∠s, AB//CD)
∠BEA=∠DEC (vert opp ∠s)
∴△ABE ~ △CDE (AAA)
Great job in proving that △ABE & △CDE are similar using the all angles equal case (AAA - refer to this chart for the cases of similar triangles)! Note that you don't really need to show the workings for the proof if the question didn't explicitly ask for it in your exam.
However, you do need to convince yourself and state that △ABE & △CDE are similar first, and then obtain the ratios of the corresponding sides (see working below) in order to solve this part 😉
∴BE:DE = AE:CE (corr ∠s, ~△s)
6:9 = AE:(35-AE)
2(35-AE) = 3AE
AE = 14 cm.
2. Another diagram to brighten things up 🙂
The altitudes of △BCE & △CDE are the same and let this altitude be h; the bases are different.
∴The ratio = (6h/2): (9h/2) = 2:3.
Yes though △BCE & △CDE are NOWHERE near similar they both share a common height h when calculating their respective areas - which then makes it easy to cancel h out when their areas are expressed as a ratio.
3. ∵△ABE ~ △CDE (from 1.)∴the ratio: 62:92 = 4:9. 62:92??? Fatty finger typo again???
This part tests your understanding of areas of similar figures i.e.
So since it's already proven in part 1 that △ABE & △CDE are similar, you can simply get the ratio of their areas by squaring the ratio of any two corresponding lengths of the triangles in one step BAM!

P.S. Make sure you're clear which is the numerator/denominator though!
4. I can tell that this appears more difficult because students would more likely focus on the six corners given. However they may ignore the angles, in which the road to success lies. Stare at this: ∠BEC=∠DEA (vert opp ∠s)
Area of △BCE = ½(6)(35-14) = 63 cm2
Area of △ADE = ½(9)(14) = 63 cm2
∴The ratio = 63:63 = 1:1.
哗……好神奇。难怪数学这么有趣!
曜
日
Some amendment in 4:
Area of △BCE = ½(6)(35-14)sin∠BEC = 63sin∠BEC cm²
Area of △ADE = ½(9)(14)sin∠DEA = 63sin∠DEA cm²
∴The ratio = 63sin∠BEC : 63sin∠DEA = 1:1.
曜
日
For Part 4, the obvious way for many would be to do it via first finding the height of each triangle using trigonometry and then calculating their respective areas like what fggffggf did.
However, for the benefit of those poor Sec Three students who've yet to learn trigo at this stage, here's another method utilizing the ratios obtained in Parts 2 and 3:
From Part 3,
Let Δ ABE = 4 units2
Let Δ CDE = 9 units2
From Part 2,
⇒ Δ BCE = 2/3 x 9 = 6 units2
Also, since Δ ABE and Δ ADE has the same base lengths (6cm and 9cm), and given they too share a common height h (similar to the case in Part 2), one can deduce that:
⇒ Δ ADE = 3/2 x 4 = 6 units2
Looking at the diagram above,

哗……数学与 Ratios 真的好神奇啊!
曜
日
我的手指不肥,因为我瘦过枝火柴,只是我打字太快罢了。