As if the world hasn’t had enough of the geek calendar, today (being 22 July) (Edit: Actually it was yesterday – couldn’t post this in time 🙁 ) happens to be Pi Approximation Day – a day to honour that often-used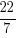 
fraction to approximate the value of π, though in reality 
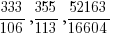etc. are actually better approximations.
Speaking of approximation, Miss Loi would like to pay a little homage on this day to this most primal and basic of mathematical topics. A topic that many of us first may have first grasped from the Granny of that classic folk song:
『三轮车，跑得快，上面坐個老太太。
要五毛，給一块，你说奇怪不奇怪！』
A topic that resurfaced later in life when a mean taxi uncle (who knew you haven’t been taught approximation in school yet) asked for $10 when the meter showed $9.70.
Or when you somehow instinctively brought along $50 to a sale to grab five items at $9.90 each, for nothing would be left if you had to return home to get more money.
Or that Miss Loi’s weight will always be 50 kg (correct to the nearest 10 kg) everytime you asked her …
In any case, do take a moment today to reflect on the following rules which are, well, supposedly so simple it’s laughable for anyone old enough not to be cheated by mean taxi uncles.
Rounding Off A Number
- Take the digit to the right of the specified (decimal) place/significant figure.
If digit < 5, drop this digit/replace with zeros to keep place value.If digit ≥ 5, add 1 to digit on the left before dropping/replace with zeros to keep place value.要五毛，給一塊, and the 三輪車 Granny is always right!
ALWAYS use/show at least 1 more decimal place/sig. fig. in your intermediate workings and only round off to the required decimal places/sig. fig. in your final answer.
CASE-IN-POINT: See Miss Loi’s O-Level ‘significant’ careless mistake
Rules of Significant Figures
- All non-zero digits (i.e. 1-9) and zeros in between them are significant.
e.g. 12 (2 sig. fig.), 12.5 (3 sig. fig.), 1.025 (4 sig. fig.) Zeros ARE significant UNLESS
- they are at the beginning of a decimal less than 1
e.g. 0.007 (1 sig. fig.), 0.071 (2 sig. fig.), 1.007 (4 sig. fig.) - *they are at the end of a whole number
e.g. *87 000 (2, 3, 4 or 5 sig. fig.), 8.7000 (5 sig. fig.)
*Depends on how estimation is made e.g.
86 999.5 ≈ 87 000 (correct to 5 sig. fig.)
86 995 ≈ 87 000 (correct to 4 sig. fig.)
86 990 ≈ 87 000 (correct to 3 sig. fig.)
86 900 ≈ 87 000 (correct to 2 sig. fig.)
86 000 ≈ 90 000 (correct to 1 sig. fig.)Note how we round off the digit to the right of the required no. of significant figures.
- they are at the beginning of a decimal less than 1
Ultimately, however, do be aware that this seemingly-innocuous topic actually harvests itself in more than half of the questions in any O-Level exam that require numerical answers, as pre-warned on the cover page of every paper (which some of you never ever read 😕 ):
- In addition, what has not (but should have) been stated in the instruction is that when it comes to money, the final answer should be in 2 decimal places (i.e. to the nearest cent) – a leading cause of grief in many exams 🙁
Also do note the following additional note in your syllabus document:
“Unless stated otherwise within a question, three-figure accuracy will be required for answers. This means that four-figure accuracy should be shown throughout the working, including cases where answers are used in subsequent parts of the question. Premature approximation will be penalised, where appropriate. Angles in degrees should be given to one decimal place.”
And in this era of foreign cyborgs and “90% to get A1!” moderation, failure to adhere to the above Commandment has often led to minor loss of marks here and there that could sadly mean the difference between grades, euphoria and despair.
But having said this, Miss Loi and some of her students have always wondered what exactly is a “non-exact numerical” answer?
What if an answer showed exactly 1.2345678 in your calculator – should you leave as such or round it off to 1.23 (3 sig. fig.)?
Hmmm … 你说奇怪不奇怪?
