 With the ongoing O-Levels, Miss Loi is heavily buried in her Mega Jφss Sticks Sessions. Please SMS or email your contact number if you’re interested in joining her classes for the new season (commencing December 2008), and she’ll call you back after the O-Levels.
With the ongoing O-Levels, Miss Loi is heavily buried in her Mega Jφss Sticks Sessions. Please SMS or email your contact number if you’re interested in joining her classes for the new season (commencing December 2008), and she’ll call you back after the O-Levels.
Thank You for your kind cooperation.
FRONTLINE UPDATE:
As forecasted, the dense fog cleared at 2.30pm this afternoon, revealing for a historical first time the likes of Partial Fractions, Double-Angle Formulae and Addition Formulae upon the A-Maths battleground.
After an agonizing informational blackout for hours, word began filtering through to The Temple:
I COULD DO ALL THE QUESTIONS! 🙂 Just hope no careless mistakes.
IT WAS OKAY I SURVIVED! Guess I could think better at the last-minute. (Miss Loi: -_-)
Can do all questions! Hehe. I hope all correct. Hehe.
I was thinking of you throughout the paper haha
And so, like last year, it appears that the enemy was annihilated in today’s opening skirmish.
Narrowing her eyes with guarded optimism, though, Miss Loi now know that the pivotal AMaths battle will be fought this Friday, where the weightage and stakes are higher, and where she knows for certain that the following heavyweights will be unleashed:
- Plane Geometry
- Curves & Circles
- Modulus Functions
- Sum & Product of Quadratic Roots
- Trigonometry – R-Formula
- Trigonometry – Factor-Formula
- Trigonometry – Equations & Graphs
- Rate of Change
- Integration – Area Under Curve(s)
- Coordinate Geometry
- You’ll still need to revise your general Differentiation, Integration, Trigonometry!
Hail to all who fought well today! Rest well and conserve your energies, for Mathematical Armageddon awaits on Friday!
Onward we march to Super Friday!
P.S. Do spare a thought and pray for Miss Loi’s lungs too as she chokes on the hundreds and thousands of joss sticks that are being burnt at The Temple in preparation for this Friday’s Mathematical Armageddon.
The wind stopped.
The whirring sound of the aircon could be heard as an eerie silence descended on The Temple, as heavy fog engulfed The Temple Gates in a proverbial calm before the storm.
Staring into the shapeless void beyond rows of students’ bags placed permanently to chope their places in The Temple this week, Miss Loi (and every single O-Level maths student out there) knows the fog will clear tomorrow and again on an action-packed Super Friday, when history shall be made as an entire generation of guinea pigs students march forth towards the first ever O-Level battle under the New Mathematics Syllabus.
Yes, once again, this is it. Time to reap the fruits of your oath.
Much of what Miss Loi wish to say has already been said last year (here and here), but here are a few more points that she would like to add:
- If you’re stuck or can’t prove the earlier part of a proving question, a Show question, or a Hence question, CONTINUE to do the next part using the ‘proven’ expression (even though you couldn’t prove it). Don’t leave the second part blank!
Remember that:
- mega/million = 106
- giga/billion = 109
- tera/trillion = 1012
- micro = 10-6
- nano = 10-9
- pico = 10-12
- Do a final practice to ensure that you know which buttons (e.g. , etc.) to use in YOUR calculator for mean and standard deviation calculations.
- Pay attention to the axes and extreme ends of the cumulative frequency curve, and be familiar with how to derive a box-and-whisker plot from it.
- Always double-check if angles in a question are in degrees or radians (when expressed in π i.e. π radians = 180°)
- When calculating arc length (s = rθ), or the area of sector (A = 1/2r2θ) i.e. that θ must always be in radians!
A-MATHS Specific
Take note of this table of the Principal Values of inverse trigonometric functions:
Function Domain Range (Principal Value) y=sin-1x -1 ≤ x ≤ 1 –π/2 ≤ y ≤ π/2 (1st & 4th quadrants) y=cos-1x -1 ≤ x ≤ 1 0 ≤ y ≤ π (1st & 2nd quadrants) y=tan-1x Real Numbers –π/2 < y < π/2 (1st & 4th quadrants) Some sample questions on this obscure but EXAMINABLE topic …
Find the principal value of sin-1(1/2).
Ans: Let sin-1(1/2) = y
⇒ sin y = 1/2
⇒ y = π/6 (In the principal value range (-π/2 ≤ y ≤ π/2), y has to be in 1st quadrant for sin y to be positive)
∴ sin-1(1/2) = π/6Find the principal value of cos-1(-1/2).
Ans: Let cos-1(-1/2) = y
⇒ cos y = -1/2
⇒ y = 2π/3
(In the principal value range (0 ≤ y ≤ π), y has to be in 2nd quadrant for cos y to be negative)
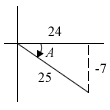
∴ cos-1(-1/2) = 2π/3If A is the principal value of tan-1(-7/24), find, without using calculator, the value of sin(-A).
Ans:

In the principal value range (-π/2 < A < π/2), A has to be in 4th quadrant for tan A to be negative, and we can obtain the values in the diagram via Pythagoras’ Theorem.From the diagram, sin A = -7/25
So sin(-A) = -sin A = -(-7/25) = 7/25
- Be familiar with the shapes of the curves of y = ax2, ax3,
 ,
,  , a√x, a 3√x and y2 = ax, for BOTH a > 0 and a < 0.
, a√x, a 3√x and y2 = ax, for BOTH a > 0 and a < 0. - Know the steps to deriving the Trigonometry R-Formula (look under ‘Deriving The R-Formula’ in the notes), especially when high marks are allocated to the part of the question.
- Go through these Plane Geometry questions one more time, for many tend to forget their own proving methods/solutions upon revisiting them.
Lastly, as Miss Loi’s handphone begins to be flooded with last-minute SMSes like this one:
Miss Loi! Do you have a Neoprint of your face for me to paste on my calculator to bring into the exam hall? I will start to remember the formulas when I see your face!
… let it be known that, while Miss Loi (and possibly her Neoprint) won’t be there in the exam hall with you, she will be there in spirit and in soul, and that you shall never walk alone.


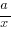 ,
, 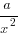 , a√x, a 3√x and y2 = ax, for BOTH a > 0 and a < 0.
, a√x, a 3√x and y2 = ax, for BOTH a > 0 and a < 0. Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 




















