A long time ago (okay not that long) in an old A-Maths Syllabus far, far away, there was an evil topic called Relative Velocity – where a mere mention of its name would strike fear into the hearts of students, caused teachers to quit, and made babies cry at night.
So one can imagine the national euphoria that reached epic proportions when the said topic was removed from the New Syllabus …
… only to be replaced by another fiendish nightmare called Plane Geometry (or Geometric Proofs to some) that’s causing widespread pandemonium for students across the nation, making teachers stutter in class, and … umm … the babies haven’t stopped crying.
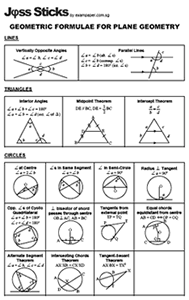
While it’s easy to say that everything you need to know is summarized in the following (along with this Similarity & Congruency chart):
The reality, however, is quite often that mortals like you and me will probably stare and stare at the Plane Geometry question till we end up like this:
But we suppose that a ‘killer’ topic like this is meant to separate the haves from the have-nots in that cumulative frquency curve, for only those on the brink of their Mathematical Nirvana will get to experience that life-changing moment of sudden realization, when you reach your Mathematical high, and your knees begin to tremble as you feel the power of the Midpoint/Intercept Theorem flowing through your body as you look up to see a glowing image of Miss Loi amongst the clouds in the sky.

If you desire to join Stephen Chow, Cristiano Ronaldo and whoever’s that Miss Universe in these emotive Plane Geometry moments, you must develop the 阴阳眼 of Plane Geometry, for the signs within those complex geometrical diagrams will only reveal themselves magically to those who possess it, and only then will you be able to ‘see’ eerie things that others don’t.
Contrary to the myth that one can only be born with it (as suspected in most foreign cyborgs cases), the 阴阳眼 (lit. Yin Yang Eye) can actually be acquired through long hours of old-fashioned practice.
To that end, Miss Loi has toiled through the week to string together the following series of Plane Geometry questions that she sincerely hope can help improve your ‘eyesight’ in time for your O-Level A-Maths papers this week.
THE PLANE GEOMETRY EYESIGHT TEST
 PLEASE DO NOT CLICK ON THE ANSWERS BEFORE YOU’VE ATTEMPTED THE QUESTION! You will NEVER be able to develop the 阴阳眼 by merely reading through the answers!
PLEASE DO NOT CLICK ON THE ANSWERS BEFORE YOU’VE ATTEMPTED THE QUESTION! You will NEVER be able to develop the 阴阳眼 by merely reading through the answers!
For a start, don’t always insist on jumping in with the latest theorems. Sometimes all you need are just the basic geometrical properties you’ve learnt in your primary school and Sec One Maths (see part 1 of this question).
Also when you see an obvious lack of circles in the diagram, be prepared to seek out and use the Intercept Theorem or the Midpoint Theorem at some point.
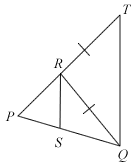
In the given figure, RT = RQ. If SR bisects ∠PRQ,
- Prove that ∠PRS = ∠RTQ.
- Show that
 .
.
[+]  ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!
ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!
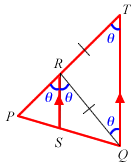
Let ∠RTQ = ∠RQT = θ (∠s of isosceles Δ)
⇒ ∠PRQ = 2θ (ext. ∠ = sum of interior opposite ∠s of Δ)Since SQ bisects ∠PRQ,
⇒ ∠PRS = ∠QRS = θ
⇒ ∠PRS = ∠RTQAnd since ∠PRS = ∠RTQ
⇒ RS // TQ (corresponding ∠s)Using Intercept Theorem,
 (∵ RQ = RT)
(∵ RQ = RT)
Instead of folding your arms and stare and stare at the diagram till you turn into stone, things can magically appear when you finally decide to lift up that 100kg pencil of yours to draw a couple of lines to join up all points in the diagram, for fortune tends to favour those who can lift and use their pencils.
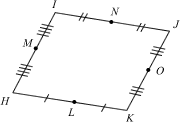
Given a quadrilateral HIJK, let L, M, N and O denote the respective midpoints. Show that LMNO is a parallelogram.
[+]  ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!
ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!
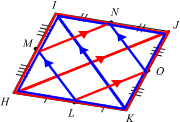
MN // MN // LO (Midpoint Theorem)
NO // IK // ML (Midpoint Theorem)
⇒ LMNO is a parallelogram (∵ MN // LO & NO // ML
Ditto for this next question. You’ll be amazed how much 天机 (Heaven’s Will) is revealed by a single (correct) stroke of fate. Moreover, you’ll also discover that most Plane Geometry solutions are pretty short (typically 1-2 steps) since each part usually carries only 3-5 marks.
It’s the 阴阳眼 that you need!
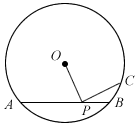
The diagram shows a circle with centre O and a chord AB. P is on AB and C is on the circle such that ∠OPC = 90°.
Prove PC2 = PA∙PB
[+]  ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!
ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!
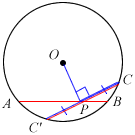
Extending the line PC to C’,
C’P = PC (Perpendicular bisector of chord)
⇒ C’P∙PC = PA∙PB (Intersecting Chords Theorem)
⇒ PC2 = PA∙PB (∵ C’P = PC)
Once again, join up the points dear – join up those points!
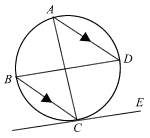
ABCD is a cyclic quadrilateral. CE is a tangent to the circle at C. Given that AD // BC, prove that
- ∠BCA = ∠DCE
- ∠ABC = ∠BCD
[+]  ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!
ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!
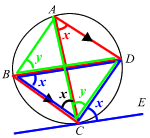
∠DCE = ∠DBC (Alternate Segment Theorem)
∠DBC = ∠DAC (∠s in same segment)
∠DAC = ∠BCA (alternate ∠s)
⇒ ∠BCA = ∠DCELet ∠DCE = x
⇒ ∠DBC = x (Alternate Segment Theorem)
⇒ ∠ACB = x (alternate ∠s)
Let ∠ABD = y
⇒ ∠ACD = y (∠s in same segment)∴ ∠ABC = x + y = ∠BCD
Have your eyes warmed up sufficiently by now? Can you now see ‘them’ now in the more complicated diagram below? Yes, they’re everywhere, crying out to you.
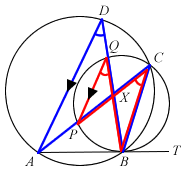
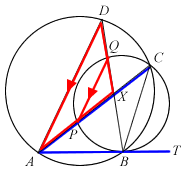
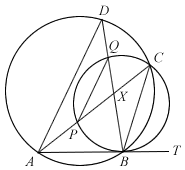 ABT is a tangent to circle PBCQ. The circles ABCD and PBCQ intersect at B and C. APC and BQD are straight lines intersecting at X.
ABT is a tangent to circle PBCQ. The circles ABCD and PBCQ intersect at B and C. APC and BQD are straight lines intersecting at X.
- Prove that PQ is parallel to AD.
- Show that
 .
.
[+]  ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!
ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!

∠ACB = ∠ADB (∠s in same segment)
∠PQB = ∠ACB (∠s in same segment)
⇒ ∠ADB = ∠PQB (corresponding ∠s)∴ PQ // AD

Since PQ // AD,
 (Intercept Theorem)
(Intercept Theorem)

Also,
AC∙PA = AB2 (Tangent Secant Theorem)

∴
And now one of the so-called ‘killer’ question to wrap things up.
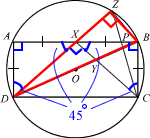
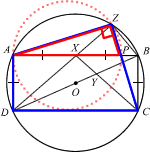
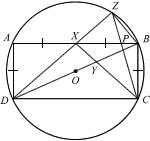 ABCD is a rectangle whose vertices lie on the circumference of a circle, centre O. X is the midpoint of AB, and AD = AX. Y lies on BD and XYC is a straight line. Z lies on the circumference of the circle and DXZ is a straight line. AC and BD intersect at O. The line CZ meets AB at P.
ABCD is a rectangle whose vertices lie on the circumference of a circle, centre O. X is the midpoint of AB, and AD = AX. Y lies on BD and XYC is a straight line. Z lies on the circumference of the circle and DXZ is a straight line. AC and BD intersect at O. The line CZ meets AB at P.
- Prove that ΔDXY is similar to ΔDZB.
- Explain why a circle that passes through A, P and Z can be drawn.
[+]  ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!
ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!

ΔDXY and ΔDZB share ∠ZDB.
∠DZB = 90° (∠ in semi-circle)
∠AXD = ∠BXC = (180°-90°)/2 = 45° (interior ∠s of isosceles Δ)
⇒ ∠DXC = 180°-45°-45° = 90° (adjacent ∠s)
⇒ ∠DXC = DZB
⇒ ∠DYX = DBZ (sum of interior ∠s of Δ)
⇒ ΔDXY similar to ΔDZB (AAA)
∠AZP = 180°-∠ADC (=90°) = 90° (Opposite ∠s of cyclic quadrilateral)
⇒ a circle that passes through A, P and Z (∵∠AZP is ∠ in semi-circle)
Most of the theorems have been covered till this point. And if you’ve successfully proven all the questions ON YOUR OWN, your knees will tremble as you receive that almighty gift of the 阴阳眼 Of Plane Geometry, knowing that no Plane Geometry question can stop you from now on.
If you don’t, you’ll just have to try the above questions all over again till you do 😉
Most importantly to all O-Level A-Maths students, may you find your 阴阳眼 in your A-Maths Papers this week!
P.S. Little Miss Loi wishes all Science students good luck for your O-Levels too!



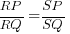 .
.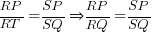 (∵ RQ = RT)
(∵ RQ = RT)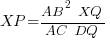 .
.
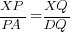
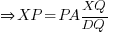
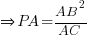
 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 




















