noise pollution in Miss Loi’s estate at 2am
Like Honda’s Type R variant of cars that appeal to Ah Beng racer boys who like to bully weave in front of Miss Loi’s demure little car on the expressways, Trigonometry has its own “Type R” model in the form of the R-Formula that was unveiled in this year’s New AMaths Syllabus.
As such students are warned to listen out for the roar of the R-Formula whenever you encounter a trigonometric question:
with an expression that contains a constant, like this:
Solve for 0° < x < 360°,
2 cot x = 3 + 2 cosec xor where you’re asked to find an expression’s max/min value, like in this rather cheong hei (long-winded) question:
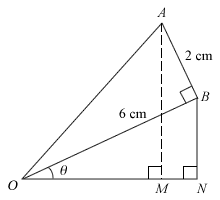
The diagram shows two right-angled triangles with their right angles at B and N. The sides OB and AB are of length 6 cm and 2 cm respectively. The lines OB is inclined at angle θ to ON. The line AM is perpendicular to ON.
- Express OM in the form OM = R cos (θ + α) and calculate the values of R and α.
- Find the value of θ for which OM = 5 cm.
- In the diagram, state the line with a length of R cm and the angle with a value α.
- Express AM in terms of R and (θ + α) and show that the area of triangle OAM is 10 sin 2(θ + α).
- Given that θ can vary, find the maximum value of the area of triangle OAM and the corresponding value of θ when this occurs.
To handle the new R-Formula questions, students need to recall the following expressions, as they will not be appearing on your formula sheet during your actual exam:
The R-Formula
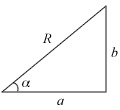
- a cos θ ± b sin θ = R cos (θ ∓ α) – look out for that inverted plus/minus!
- a sin θ ± b cos θ = R sin (θ ± α)
where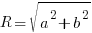 
and 
and 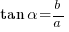a > 0, b > 0, α is acute
Maximum/Minimum Values of R-Formula Expressions
- The maximum value is R which occurs when cos/sin (θ ± α) = 1
- the minimum value –R which occurs when cos/sin (θ ± α) = -1
Deriving The R-Formula
Do note that the R-Formula highlighted above is NOT a given, especially when the relevant part of the question carries a high weightage of marks e.g.
There’s a bit of debate on this but don’t think you can get away with all 6 marks here by simply substituting the values into the R-Formula! So to be a little kiasu, it’s advisable to derive the whole thing as per the following steps:
4 cos θ – 3 sin θ
= R cos (θ+α)
= R [cosθcosα-sinθsinα] (Addition Formula)
= (R cosα)cosθ-(R sinα)sinθ
Comparing coefficients between LHS & RHS,
R cosα = 4 —– (1)
R sinα = 3 —– (2)
(2)/(1): tan α = 3/4 ⇒ α = 36.9°
(1)2+(2)2:
R2cos2α+R2sin2α = 42+32
R2[cos2α+sin2α] = 25 ⇒ R = 5
∴ 4 cos θ – 3 sin θ = 5 cos(θ+36.9°)
Important Notes
To reiterate what was stated above, a and b MUST be positive. DON’T do this:
(-3) cos θ + (-2) sin θ = 3 → WRONG!
Instead, move the terms around to ensure that the first term is always positive:
3 cos θ + 2 sin θ = -3 → CORRECT! YAY!
Please, please, please, please, please for the addition cases (i.e. a cos θ + b sin θ or a sin θ + b cos θ) you can simply re-arrange the sine and cosine terms depending on how you wish to express the R function in your question.
E.g.
3 cos θ + 2 sin θ → if you require R cos (θ – α)
2 sin θ + 3 cos θ → if you require R sin (θ + α)
Hailed as the pinnacle of O-Level Trigonometry, a typical R-Formula question may also require your skills on lesser trigonometry variants such as the Addition Formulae, or the Double Angle Formulae, or the Factor Formulae, together with your knowledge of basic angles (e.g. in question 1 above when you’re asked to find all angles within the range of blah blah blah).
But once you tame it, you’ll be rewarded with a straightforward ride and zoom away with plenty of marks.
So are you ready to test-drive your R-Formula with the two questions above? Miss Loi doesn’t expect you to crash this in your O-Level in two weeks’ time!
*Zooms away for Jφss Sticks Sessions (Type-R variant)*
N.B. Once again, Miss Loi does NOT advocate nor encourage speeding or any form of street racing in Singapore.
