These aliens are often friendlier than they look.
*Puts on helmet*
*SHOWS STERN & MEAN FACE*
*Sounds bugle* EVERYBODY WAKE UP!
Sergeant Loi is back from her May Day leave – only to find The Temple in a state of 兵慌马乱 as the mid-year exams loom.
To whip everyone back to shape, Sergeant Loi shall complete the trinity (which began with indices, and followed by logarithms) with the concluding drill on surds today!
Despite the scary-looking longish workings, surds are the most straightforward part of the trinity. For most parts, the TWO main things you’ll ever need to know are how to simplify (with a dose of trial-and-error common sense) and rationalise surd expressions.
That’s it! Now let’s go eat some surds for breakfast!
*Cracks whip*
The Rationale of Surds
A. WHAT IS A SURD?
High-class definition:
An irrational root of a real number. *sweats*
Simple O Level definition:
A *square-root of a number that results in endless decimal places when you press your calculator e.g.
- √2 is a surd (=1.4142135623 … when you press your calculator)
- √9 is NOT a surd (= 3 when you press your calculator – WOW NO DECIMALS!)
*Actually can also be cube-root, nth-root etc. but let’s not go there …
B. THE OPERATIONS OF SURDS
*Compare operations B(2) & B(3) to the Rules of Indices (Part C) and you’ll realize they’re like long-lost twins!
e.g. Simplifying surd expressions:
- √18 = √(9 × 2) = √9 × √2 = 3√2
→ Using B(2) and a tiny bit of trial and error to get the (9 × 2) - 3√2 + 5√2 = (3 + 5)√2 = 8√2 → Using B(4)
- (√5 – √2)2 = (√5 – √2)(√5 – √2)
= √5√5 – √5√2 – √2√5 + √2√2
= 5 – √10 – √10 + 2 → Using B(1) + B(2)
= 7 – 2√10 → Using B(4)
 DON’T ever do this:
DON’T ever do this:√(a+b) ≠ √a + √b → WRONG!
√(a–b) ≠ √a – √b → WRONG!
e.g.
√64 ≠ √32 + √32!
√25 ≠ √12 + √13!
C. CONJUGATE SURDS
(Note the MINUS sign on the RHS)
e.g. (√3 + √2)(√3 – √2) = 3 – 2 = 1
 DON’T ever do these:
DON’T ever do these:(√a – √b)2 ≠ (√a2 – √b2) → WRONG!
(√a + √b)(√a – √b) ≠ (√a)2 + (√b)2 → WRONG!
D. RATIONALISING THE DENOMINATORS OF SURDS
Having a surd in the denominator is IMPROPER, UNGLAM, SINFUL & IMMORAL!!!
So we need to rationalise the denominators by multiplying the top and bottom by the same number with respect to the denominator i.e.
- If denominator consists of a single term → multiply top & bottom by denominator term e.g.

If denominator consists of 2 terms → multiply top & bottom by conjugate of denominator e.g.


SAMPLE PRACTICE QUESTIONS
- Simplify
 .
.Ans:

→ multiply top & bottom with conjugate surds (C)


- Given that
 , find the value of k.
, find the value of k.Ans:
→ Rationalize all the sinful terms with surds in denominator!



→ Now simplify the surds using B(2) above and a tiny bit of trial and error



→ split √6 into √2√3 since we’re going to compare with the √3 term on RHS


 via comparing coefficient of √3
via comparing coefficient of √3
As always, get these rules drilled into your head! Spot the pointers and common mistakes in red! Understand the representative sample questions! Check out more surds in action!
Print this out if necessary and remember the above procedures by heart, for if you fail in rationalizing surds in your exams, you’ll need to write a 1000000-word essay to Sergeant Loi explaining the rationale for not punishing you!
*Cracks whip*

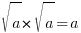
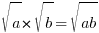
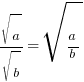
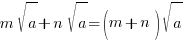
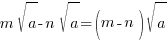
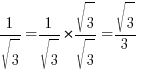
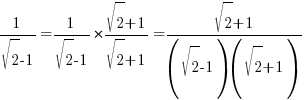
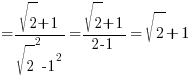
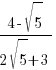 .
.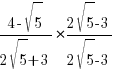
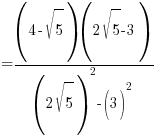
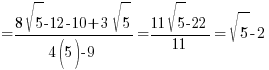
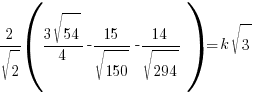 , find the value of k.
, find the value of k.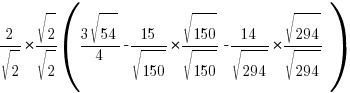
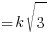
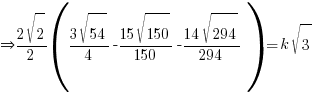
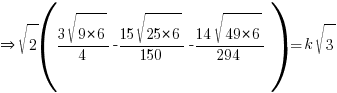
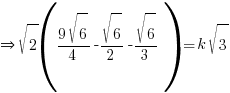
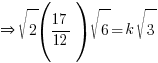
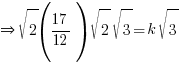
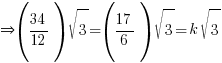
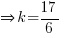 via comparing coefficient of √3
via comparing coefficient of √3 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 




















