
to defeating Partial Fractions
*Puts on helmet*
*SHOWS STERN & MEAN FACE*
*Sounds bugle* EVERYBODY FALL IN!
Today you’ll learn to deal with a new enemy originally from the A-Level campaign. Something never been seen by your previous O-Level comrades, nor has it appeared in the pages of the old Ten-Year Series 武林秘籍 (ala Secret Manual).
But fret not! Though it looks formidable at first, its size also makes it unwieldy and predictable, so master the rules of engagement (see A. and B. below) and follow the standard 三大招式 (Three Devastating Moves) detailed in each of the Sample Questions below, and you’ll be on your way to defeating these Partial Fractions!
NOW ALL TURN TO PAGE 1 OF YOUR 武林秘籍 (2008 revised edition)!!!
*Cracks whip*
Frag The Partial Fractions!
A. COMPULSORY PRE-CHECK
The degree of a polynomial is the highest power of x. e.g.
p(x) = 4x3 – 12x2 – x – 4 ⇒ degree = 3
q(x) = (x – 1)(x + 2) ⇒ degree = 2 ( ∵ when expanded q(x)=x2+x-2)For
 :
:- if degree [ p(x) < q(x) ] ⇒ PROPER ⇒ proceed with main Partial Fraction calculations (YAY!)
- if degree [ p(x) ≥ q(x) ] ⇒ IMPROPER ⇒ Long Division Time! (see Qn 2 below) (SIANZ!) (note it’s greater OR EQUAL)
B. THE RULES OF PARTIAL FRACTIONS ENGAGEMENT
For 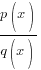 : (*Have you ‘propered’ this first? See above.)
: (*Have you ‘propered’ this first? See above.)
| Rule | If q(x) contains | Partial Fraction must contain |
|---|---|---|
| 1 | linear factor (ax+b) | 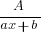 for each linear factor for each linear factor |
| 2 | repeated linear factor (ax+b)2 | 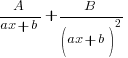 for each repeated linear factor |
| 3 | quadratic factor x2+c2 | 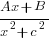 for each quadratic factor |
 (x2 – b2) can be factorized further into (x + b)(x – b)
(x2 – b2) can be factorized further into (x + b)(x – b)
→ two linear factors! (≠ quadratic/repeated linear factor!)
SAMPLE PRACTICE QUESTIONS
(Note the standard 三大招式 steps).
Express
 in partial fractions.
in partial fractions.Ans:
- 第一式 (绝招)
Check: degree of (7x+4) = 1 < degree of (2x+1)(x-2)2 = 3
⇒ PROPER (YAY!) - 第二式
So

→ 1 x linear factor (2x+1) and
→ 1 x repeated linear factor (x-2)2Using Rules 1 & 2 from the table above, we have:

*Note there’re two components for the repeated linear factor (x-2)2!
- 第三式 (绝招)
Multiply both sides by (2x+1)(x-2)2,
7x+4 = A(x-2)2 + B(2x+1)(x-2) + C(2x+1)To find A, B and C, sub in suitable values for x that makes certain components disappear:
Sub x = 2,


Sub x =
 ,
,


Sub x = 0, A =
 , C =
, C =  ,
,


Hence,


- 第一式 (绝招)
Express
 in partial fractions.
in partial fractions.Ans:
- 第一式
Check: degree of (x4+9) = 4 > degree of (x3+3x) = 3
⇒ IMPROPER ⇒ LONG DIVISION TIME!!! (SIANZ! 🙁 )
- 第二式
Now
 can be factorized further to
can be factorized further to 
→ 1 x linear factor (x) and
→ 1 x quadratic factor (x2+3)Using Rules 1 & 3 from the table above, we have:

*Note: all we need is the quotient (x) from the long division in i.
- 第三式
Multiply both sides by x(x2+3),
x4+9 = x2(x2+3) + A(x2+3) + (Bx+C)xTo find A, B and C, sub in suitable values for x that makes certain components disappear or your life easier:
Sub x = 0,
⇒ 9 = (0)(3) + A(3) + (C)(0)
⇒ A = 3Oh we can’t reduce other components to 0 with another substitution → need simultaneous equations here:
Sub x = 1 (to make your life easier), A = 3,
⇒ 1+9 = (1)(4) + (3)(4) + B + C
⇒ B + C = -6 —– (1)Sub x = -1 (to make your life easier), A = 3,
⇒ 1+9 = (1)(4) + (3)(4) + (-B + C)(-1)
⇒ B – C = -6 —– (2)Solving (1) & (2),
B = -6, C = 0Hence,

- 第一式
As always, get these rules drilled into your head! Spot the pointers and common mistakes in red! Understand the representative sample questions!
Print this out if necessary and remember the above procedures by heart, for if you don’t Sergeant Loi will unleash her own version of the 三大招式 upon you!
*Cracks whip!*

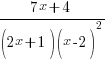 in partial fractions.
in partial fractions.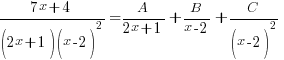
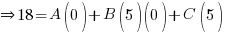
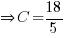
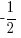 ,
,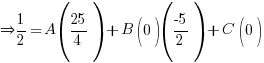
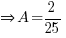
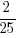 , C =
, C = 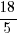 ,
,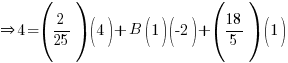
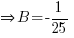
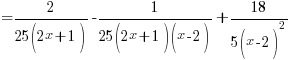
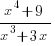 in partial fractions.
in partial fractions.
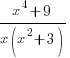
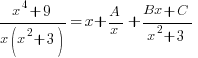
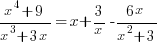
 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 




















