
to a log (and tickle your bare feet)!
*Puts on helmet*
*SHOWS STERN & MEAN FACE*
*Sounds bugle* EVERYBODY FALL IN!
Today’s drill is going to be a little longer (and tougher) than the previous one, since so many of you were tragically killed in action at logarithmic minefields over the years.
So to prevent yourself from adding to the end-of-year body count, get ready for Log PT!
PICK UP YOUR LOGS NOW! EXERCIIIIIIISE BEGIN!
*Cracks whip*
The Laws of Logarithms
A. IF YOU DON’T KNOW THESE, CAN CLOSE SHOP & FORGET ABOUT THE REST!
For
 to be defined y > 0 AND a > 0*This property is often used to select possible values of y when a logarithmic equation has more than one solution.
to be defined y > 0 AND a > 0*This property is often used to select possible values of y when a logarithmic equation has more than one solution.


 → This is what the log key does on your calculator!
→ This is what the log key does on your calculator! → This is what the ln key does on your calculator!
→ This is what the ln key does on your calculator!From (2) above, you can deduce that:
 and
and 
From (3) above, you can deduce that:
 and
and  → many forget this!
→ many forget this!
B. THE OFT-MISUNDERSTOOD LAWS OF LOGARITHMS
- PRODUCT LAW:

 DON’T ever do these:
DON’T ever do these:
 → WRONG!
→ WRONG!
 → WRONG!
→ WRONG! - QUOTIENT LAW:

 DON’T ever do these:
DON’T ever do these:
 → WRONG!
→ WRONG!
 → WRONG!
→ WRONG!
 → WRONG!
→ WRONG! - POWER LAW:

 DON’T ever do this:
DON’T ever do this:  → WRONG! (note the brackets)
→ WRONG! (note the brackets) - CHANGE-OF-BASE LAW:

 DON’T ever do this:
DON’T ever do this:  → WRONG!
→ WRONG!
e.g. ≠
≠  !
!
Instead it should be
SAMPLE PRACTICE QUESTIONS
Solve
 .
.Ans:

→ using Change-of-Base Law from B(4) above (remember that c can be any arbitrary value)


→ using Power Law from B(1) and from A(2) the denominator .
.
 .
.

→ using Power Law from B(1) again.

→ CAN cancel both sides since both logs are of the same base.
… the rest you should be able to solve on your own!The mass, m of a radioactive substance, at time t days after being first observed, is given by the formula
 . Find the value of t when the mass is half of its value at t = 0.
. Find the value of t when the mass is half of its value at t = 0.Ans:
When t = 0,
 → somehow many fail to realize this
→ somehow many fail to realize thisWhen m is half of m when t = 0,




→ ln both sides when you’re typically looking for a x in ex

→ Using Quotient Law from B(2) for L.H.S. and Power Law from B(3) for R.H.S.

→ since ln 1 = 0 from A(3) and ln e = 1 from A(6) above

As usual, get these rules drilled into your head! Spot the pointers and common mistakes in red! Understand the representative sample questions! Check out this question for further practice!
Print this out if necessary and stay on the right side of the laws above – for if you don’t Sergeant Loi will literally tie you to a log and unleash unspeakable terrors (e.g. tickling your bare feet) upon you!
*Cracks whip!*

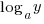 to be defined y > 0 AND a > 0
to be defined y > 0 AND a > 0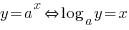
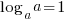
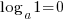
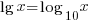
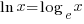
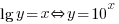 and
and 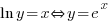
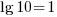 and
and 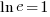
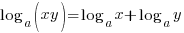
 DON’T ever do these:
DON’T ever do these: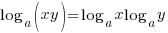 → WRONG!
→ WRONG!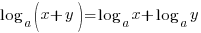 → WRONG!
→ WRONG!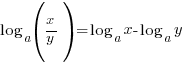
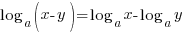 → WRONG!
→ WRONG!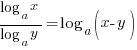 → WRONG!
→ WRONG!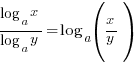 → WRONG!
→ WRONG!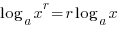
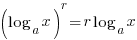 → WRONG!
→ WRONG! 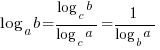
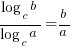 → WRONG!
→ WRONG!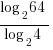 ≠
≠ 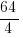 !
!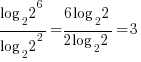
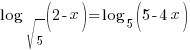 .
.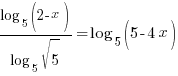
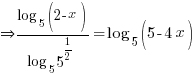
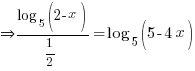
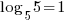 .
.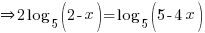 .
.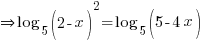
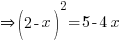
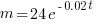 . Find the value of t when the mass is half of its value at t = 0.
. Find the value of t when the mass is half of its value at t = 0.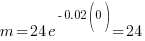
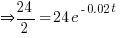
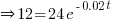
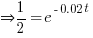
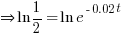
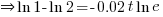
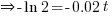
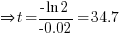
 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 




















