Tucked neatly within the (hopefully) crinkled pages of your A-Maths textbook is a little chapter called Binomial Theorem. An innocuous chapter that nevertheless managed to inspire one of the greatest pieces of mathematical working mankind has ever witnessed:
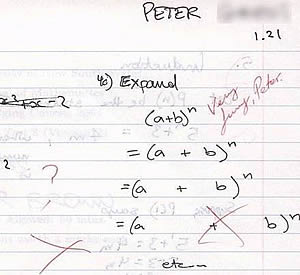
Unfortunately, by this act the great Peter also managed to inspire whole generations of hardcore LMBFH Syndrome suffering students to skip this chapter altogether because it “Looks so difficult! Somemore will only come out once! No time already! Must skip!”.
A pity really, as being one of those *tak glam chapters its questions are usually pretty straightforward, compared to those from its bigger, more glamourous cousins like Functions, Trigonometry, Circular Measure etc. who often have a habit of ganging-up on you.
In fact, Binomial Theorem questions typically only require you to either
- expand an expression OR
- find a specific term in an expansion
So … which kind of question do you think this is?
Given that the expansion of (a+x)(1-2x)n in ascending powers of x is 3- 41x + bx2 + …, find the values of the constants a, n and b.
Now ALL that you need to remember, as far as A-Maths Binomial Theorem goes, is:
(a+b)n = an + nC1an-1b + nC2an-2b2 + … + nCran–rbr + … + nCn-1abn-1 + bn
where nCr =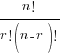 
and the (r+1)th term (Tr+1) of the expansion is highlighted in red.
That’s it. All those labyrinthine pages of unintelligible hieroglyphs in your textbook nicely contained in one cute orange box.
The key to the above question is to know how far to expand the expression, since we’re dealing with an unknown n. For this obvious reason, blur students might be startled to discover that you can’t use the nCr button on your calculator anymore.
In her kindness, Miss Loi shall go further and simplify the three most commonly used nCr expressions for you to remember, so you don’t have to ponder from scratch each time:
nC1 = n
nC2 =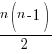 
nC3 =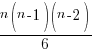 
Now if only Peter had known all these, the world would’ve been a much less interesting place.
*Local colloquial for unglamourous.
