Apparently the last Functions question was quite a QED.
So on a dark overcast day, Miss Loi was looking around for something a little more challenging, when a clairvoyant voice suddenly boomed in her head:
Miss Loi! Thou shalt post that Functions question on thy blog!
Slightly startled, Miss Loi looked up to the skies in the direction of the voice, and traced it to a break in the clouds where rays of light emanated from.
“But that question has only been seen once in the autumn of 2002. Besides that’s a premium question where mortals seldom tread.” she answered meekly.
The Darth Vader-like voice retorted sharply:
That is why, my sexy young tutor, post it up thou must! For this is the final year for the existing functions syllabus, and the constellations have aligned. I fear the time is nigh for it to appear again!
So here’s the premium Functions question, courtesy of some orders from above, which will will lead to a marshmallow popping into your mouth if you can get it right on the first try at The Temple:
The function f(x) = x3 + ax + b is such that the equation f(x) = x has solutions x = 1 and x = 2.
- Find the values of a and b.
- With these values of a and b, determine whether the curve y = f(x) has any turning points and hence explain why the inverse function exists for x ≥ 2.
- Evaluate f-1(15).
Mama drama aside, this is meant to test your understanding of inverse functions. Questions like this one (especially part 2 here) will usually require you to memorize and regurgitate the following Golden Phrase at some point in your answer:
The inverse of function f exists if f is one-to-one
For those who have been confused by the non-human definitions of one-to-one and many-to-one functions in textbooks/notes till now, this diagram will hopefully help settle the issue once and for all:
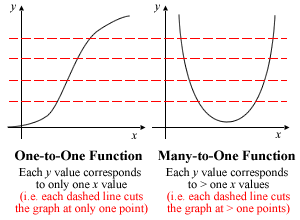
For the premium part (i.e. part 3) of this question, note that f(x) is a cubic function, so you can’t use the usual let y = f(x) to find the inverse.
Instead it tests your understanding of this:
Domain of f-1 = range of f; range of f-1 = domain of f.
Actually it’s really quite simple once you know what to do. But Miss Loi better stop here as she has spoken too much already. 天机不可泄漏!
DISCLAIMER: Though the constellations may indicate otherwise, Miss Loi makes absolutely NO guarantee that the above question will appear in your upcoming O-Level exam. Moreover, the sky was nowhere near overcast today.
