As typical Singaporeans, we all love our AIO packages. From wash/cut/treatment/rebond/blow/dry hair salon packages to body scrub/facial/massage/honey milk bath spa packages, they usually offer (in theory) better value over the sum of their parts.
In exams, however, evil AIO packaged questions (i.e. those that test you knowledge of multiple topics in one go) offer students plenty of nail-biting moments and the unique opportunity to experience a panic attack.
As a sadist an esteemed educator, it is perhaps natural that Miss Loi has a mild fetish for a question like this:
N.B. This is E-Maths Paper One so NO CALCULATORS ALLOWED!
A, B and C are the vertices of an equilateral triangle which lie on a circle of radius r cm. Using as much information given in the table below as necessary,
| sin | cos | tan | |
| 60o | 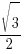 | 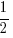 | √3 |
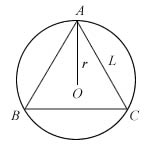
- Show that the length L cm, of a side of ΔABC is r√3 cm
- By comparing the area of ΔABC and the circle, or otherwise, show that 3√3 < 4π.
- List all even integers in the range of 3√3 to 4π.
There you have it.
Something to send you scurrying up and down the chapters of that imaginary textbook in your overworked mind.
Rejuvenated by her facial package yesterday, Miss Loi shall be nice this time and hint that for this particular one, you should bookmark the chapters on Trigonometry, Rational/Irrational Numbers and Mensuration (for once, let’s not joke about this chapter title ok?).
In addition, you’ll need in abundance material from another chapter not found in your book called Common Sense.
But frankly, once you know what you’re supposed to do, this question is actually pretty easy. Hence no formula listed here this time to spoil the fun!
