Chief Stewardess of The HMS Buddha Foot.
Though Miss Loi wished otherwise.
Dear passengers, thank you for sailing with Temple Cruises and welcome aboard the HMS Buddha Foot now departing Bangkok for Singapore. This is your Chief Stewardess Miss Loi speaking.
First of all, a big apology to all passengers transferred here from Flight JS296. Unfortunately as prophesied, the Flight Captain extended his Thai massage timing and now there’s no pilot to fly us back to Singapore. And no way Miss Loi would want to go through another near-death experience with you!
*Nokia ring tone* Oops … excuse me. Yes dear, what’s up?
*unintelligible babble*
You said WHAAAAT????!!! And you want me to tell them that? Ok ok …
I’m terribly, terribly sorry! Our Cruise Captain, with his dashing farang features, has just been ripped off by the farang prices at the harbour fuel station! As such we only have enough fuel to get us stranded in the middle of the South China Sea, where evil pirates plunder unfortunate ships and abduct entire crews of kawaii sailormoon-clad stewardesses!
But fret not! We’ve sent out an SOS an a refueling ship is on her way meet us somewhere to top up our fuel.
Problem is, after spending the whole of last night in some sleazy Bangkok bar, your Captain is not really in the right mathematical frame of mind to calculate where this somewhere might be. This, though, is what he said over the phone:
Our cruise ship is now at the point with position vector (i + 12j) km and is cruising with a velocity of (30i + 20j) km/h.
At this moment, the refueling ship sets off at the point with position vector (85i + 5j), with a velocity of (-50i + kj), where k is a constant.
What must be the value of k in order for the two ships to meet?
Now close the pages of your Passenger’s Handbook as chances are this will not be found there.
Instead, Use the Force, Luke. Trust your feelings. close you eyes and think …
Stuffs like position vectors and i and j indicate to you that this is the other kind of Relative Velocity problem which is solved through vectors.
Compared to the trigonometry kind, this is much easier provided you remember this:
Position vector of an object P at time t, relative to an origin O, traveling at a constant velocity v can be represented by:
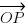+ vt
where 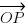represents the initial position of P.
Couple this with your elementary knowledge of column vectors, and you shouldn’t even need to draw a diagram.
So can anyone save the HMS Buddha Foot and her crew of kawaii sailormoons from being stranded in the high seas and becoming a sitting duck for meanies like him?
