Mom and Dad will forever nag about the importance of being a goody two shoes and staying away from shady characters in shady areas. However, the A-Maths Syllabus dictates that every student’s integral-ity be tested by making him/her venture at least once into such areas during the exams. Hur hur hur.
The following question is designed to sieve out the street-smart students from the horribly naive, pampered, and unworldly ones (aren’t we all):
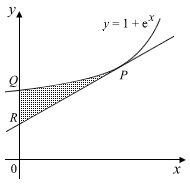The diagram shows part of the curve y = 1 + ex, intersecting the y-axis at Q. The tangent to the curve at the point P(1, 1+e) intersects the y-axis at R.
Find the area of the shaded region PQR.
Upon first glance, many of Miss Loi’s students will go: “Walau! So simple! Just integrate the curve to get the area beneath bounded by the points Q and P, and then integrate the straight line to get the area beneath bounded by the same x-coordinates for points R and P, and then subtract the two areas can already!”.
Miss Loi: “So how are you going to integrate that straight line without knowing its equation?”
Student: *frantically flips textbook for chapters on Differentiation and Coordinate Geometry*
