Jφss Sticks Tuition Centre

“Baby, baby, baby ohh … I thought you’d always be mine”, those emo words from Justin ~~Bear Bear~~ ~~Bebe~~ ~~Barber~~ Whoever’s Youtube video rang agonizingly off the study room walls as he stared in vain at his A-Maths notes.

Fresh from a breakup with a girl he’d known since he was 13, he found his eyes constantly flitting from his depressingly boring binomial theorem notes towards a depressingly heartbreaking Neoprint of the two of them taken at Bugis Junction in happier times.

With less than a month to the A-Maths Paper, he’s deep into Last-Minute Buddha Foot Hugging territory. But tried as he might, the scholarly, geeky student just couldn’t focus and that endlessly-looping chorus certainly didn’t help his droopy eyes …

The Geeky Tutor

Suddenly the song stopped and a breeze chilled the air in the room, following which he nearly jumped off his chair when he opened his eyes to the sight of a young bespectacled girl seated next to him.

*GASP* Who on EARTH are you?!!!

I’m Miss Loi. Your new maths tutor. Sorry to have startled you.

What??? Tuition now? It’s almost midnight!

With the exams so near and seeing you struggling to get over your breakup, your Mom called my tuition centre for help. Unfortunately we are full but my Sensei decided to send me, an intern tutor, to help you as part of my training. However I can only make it on very late nights so here I am.
Anyway since you seem to be diligently onto your Binomial Theorem notes right now (an oft-misunderstood topic that scared off lots of students due to its complicated and tedious-looking workings at first glance), let’s start on that shall we?

DEMYSTIFYING BINOMIAL THEOREM

The Binomial Expansion

$(a+b)^n = a^n + (matrix{2}{1}{n 1})a^{n-1}b + (matrix{2}{1}{n 2})a^{n-2}b^2 + cdots + (matrix{2}{1}{n r})a^{n-r}b^r + cdots + b^n$
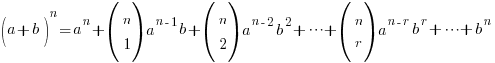
This is given in the formula sheet – don’t waste your brain cells memorising it!

Expression for the `r`+1^th term

$T_{r+1} = (matrix{2}{1}{n r})a^{n-r}b^r$

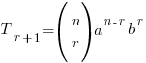
This is NOT given in the formula sheet – but if you can’t remember it you can easily ‘extract’ it from the main binomial expansion expression: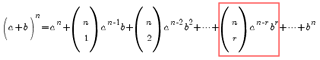

Don’t simply assume the r+1^th term T_r+1 is “the term in x^r “!

The enigmatic “term independent of x“ and the “constant term” both refer to the term that contains x⁰.

Don’t always rush in headlong like a mad dog unleashed to expand the entire expression. Instead, keep the T_r+1 expression in mind when asked to find or compare coefficients of specific terms.

The ⁿC_r Formula

That 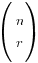in the binomial expansion is not a matrix. Instead it’s given in the formula sheet as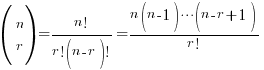

Many students, however, ignore the above ~~KPKB~~ exclamation-laden expression and simply press the nCr button on their calculators – only to meet a tragic end when n is unknown in the question.

So for the sake of the questions where n is unknown, it’s worthwhile to be familiar with the following expressions for up till *ⁿC₄:

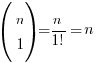
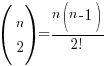
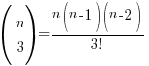
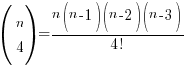
*Most O Level AMaths binomial questions only require you to deal with up to the first 4 terms, but don’t take my word for it 🙂 In any case, you should be able to ‘see’ the pattern for the expressions and use the x! button on your calculator to find that factorial (!) in the denominator if you need to obtain ⁿC_r expressions beyond the first 4 terms.

OK this, plus a firm grasp of your Rules of Indices, is ALL you need to know for Binomial Theorem!

Huh? That’s all? Like this I can also be a tutor myself! I wonder why Mom decided to engage you … hey where have you gone???

The student looked up to find that she had suddenly vanished.

I’m not done yet.

Turning around, he nearly fell off from his chair again at the sight of her seated behind him.

The Four Basic Binomial Theorem Questions

‘O’ Level AMaths binomial questions generally fall into four types, though a combination of them may be asked within the same question:

[+] A. Expand & Multiply

This is the classic binomial question where you expand an expression up to the first couple of terms, and then use your partial expansion to obtain the expansion of more a complicated expression. You may or may not be told how many terms to expand to, but you almost always should NEVER attempt to expand the entire expansion, especially if the powers are high.

Find, in ascending powers of x, the first 3 terms in the expansion of
(a) (1 + 4x)⁶ (b) (1 − 2x)¹⁴

Hence find the expansion of (1 + 4x)⁶(1 − 2x)¹⁴ up to the terms in x².

ANS: Using the Binomial Expansion formula given in your formula sheet,

(a) (1 + 4x)⁶
= 1⁶ + ⁶C₁(1⁵)(4x) + ⁶C₂(1⁴)(4x)² + …
= 1 + 6(1)(4x) + 15(1)(16x²) + …
= 1 + 24x + 240x² + …

(b) (1 − 2x)¹⁴
= 1¹⁴ + ¹⁴C₁(1¹³)(−2x) + ¹⁴C₂(1¹²)(−2x)² + …
= 1 − 14(1)(2x) + 91(1)(4x²) + …
= 1 − 28x + 364x² + …

To obtain the first 3 terms of (1 + 4x)⁶(1 − 2x)¹⁴, we multiply and expand (1 + 24x + 240x² + …)(1 − 28x + 364x² + …) but we must know when to stop multiplying!

Know when enough is enough!

Since we’re only interested in terms up to x², we ignore all combos that result in powers of x > 2 and kick them into oblivion for trying to waste your precious exam time!

(1 + 24x + 240x² + …)(1 − 28x + 364x² + …)
= 1(1 − 28x + 364x²) + 24x(1 − 28x ~~+ 364x²~~) + 240x²(1 ~~− 28x + 364x²~~)
= 1 − 28x + 364x² + 24x − 672x² + 240x²
= 1 − 4x − 68x²

This is when your intimate knowledge of indices is called upon, especially with trickier expressions containing more than one x and inverse powers of x e.g. $(x^3 - 2/{x^2})^10$

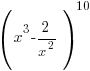
Sometimes you’re NOT told how many terms to expand, but simply told to e.g. “expand up to and including the terms in x³” or “given that (1 + 4x)⁶(1 − 2x)¹⁴ = a + bx + cx² + …, find a, b and c.” In such cases, you’re expected to know from the start how many terms to expand to, but for the sake of your future NEVER, EVER kill yourself by trying to expand the entire expression, especially when the powers are high e.g. (1 − 2x)¹⁴

Tekan Revision Exercise

Find the term independent of x in the expansion 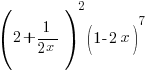$(2+1/{2x})^2(1-2x)^7$ .

[Answer: −3]

[+] B. Expand & Substitute

Instead of ‘Expand & Multiply’ describe above, this time you expand and substitute a suitable value/expression into your expansion in order to expand a more complicated expression, estimate a value, ~~and achieve world peace~~.

Expand (1 − p)⁵. Use this result to find the expansion of (1 − x + x²)⁵ as far as the term in x³. Use a suitable value of x to estimate (1.11)⁵ from this expansion.

ANS: Using the Binomial Expansion formula given in your formula sheet,

(1 − p)⁵
= 1⁵ + ⁵C₁(1⁴)(−p) + ⁵C₂(1³)(−p)² + ⁵C₃(1²)(−p)³ + ⁵C₄(1²)(−p)⁴ + (−p)⁵
= 1 − 5p + 10p² − 10p³ + 5p⁴ − p⁵

Do the Substitution!

To make (1 − x + x²)⁵ be like (1 − p)⁵, we equate 1 − p with 1 − x + x²:
⇒ 1 − p = 1 − x + x²
⇒ p = x − x² → our substitute expression!

So sub p = x − x² into the expansion:
= 1 − 5(x − x²) + 10(x − x²)² − 10(x − x²)³ ~~+ 5(x − x²)⁴ − (x − x²)⁵~~
→ we’re only interested in terms up to x³, so we ignore all combos that result in powers of x > 3 to save time
= 1 − 5x + 5x² + 10(x² − 2x³ ~~+ x⁴~~) − 10(x³ ~~+ …~~)
→ Yay! Don’t have to expand that cubic expression as there’s only one x³ term in (x² − 2x³ + x⁴)(x − x²)
= 1 − 5x + 5x² + 10x² − 20x³ − 10x³ + …
= 1 − 5x + 15x² − 30x³ + …

Substitute again!

To estimate (1.11)⁵ using x, we equate 1.11 with 1 − x + x²
⇒ 1.11 = 1 − x + x²
⇒ x² − x − 0.11 = 0
Solving the quadratic equation, x = −0.1 or 1.1

In order to use (1 − x + x²)⁵ = 1 − 5x + 15x² − 30x³ + … to estimate (1.11)⁵, it’s better to use x = −0.1 since its higher powers are comparatively smaller enough to be ignored i.e. −0.1⁴ = −0.0001 vs 1.1⁴ = 1.4641

∴ (1.11)⁵ ≈ 1 − 5(−0.1) + 15(−0.1)² − 30(−0.1)³ ≈ 1.68

[+] C. Finding Specific Terms

This is the kind of question where you’re asked to find “the term in x¹⁰“, “the term independent of x“, “the constant term”, “the coefficient of x⁴” etc. from a straightforward (a + b)ⁿ expression (vs the multiplied (a + b)ⁿ(c + d)^m in preceding examples).

This is when the r+1^th Term formula must instantly possess your mind, so that you curb your expansionary instincts and control yourself – don’t rush in blindly like a mad dog unleashed to expand the entire expression to the detriment of your precious exam time!

In the expansion of 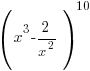$(x^3 - 2/{x^2})^10$ , find
(a) the term in x¹⁰
(b) the coefficient of $1/{x^5}$
(c) the constant term

ANS: This is a straightforward (a + b)ⁿ expression ⇒ NO expansion is necessary (Control yourself! You don’t want to die young expanding this to the power of 10!)

Derive the General `T`_r+1 ‘Formula’ for the Expression

The key is to first derive a general T_r+1 ‘formula’ for this from the r+1^th Term formula and simplify it using, once again, some indices magic:
$T_{r+1} = (matrix{2}{1}{10 r})(x^3)^{10-r}(-2/{x^2})^r$
${} = (matrix{2}{1}{10 r})x^{30-3r} (-2)^r x^{-2r}$
${} = (matrix{2}{1}{10 r}) (-2)^r x^{30-5r}$

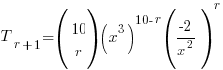
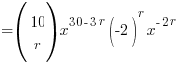
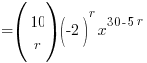
⇒ power of x = 30 − 5r

And now, armed with this almighty expression for the power of x, you find yourself in ‘God Mode’ where, by a simple substitution of r with a suitable value, nothing, absolute nothing, can stand between you and the solutions to parts (a), (b) and (c) 😈 Muahahaha!

(a) For x¹⁰, 30 − 5r = 10 ⇒ r = 4
∴ term in x¹⁰ = 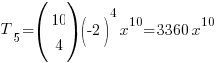$T_5 = (matrix{2}{1}{10 4})(-2)^4 x^10 = 3360x^10$ (Muahahaha!)
→ x¹⁰ is included in the final answer since we are finding the term

(b) For x⁻⁵, 30 − 5r = −5 ⇒ r = 7
∴ coefficient of x⁻⁵ = 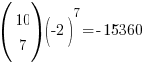$(matrix{2}{1}{10 7})(-2)^7 = -15360$ (Muahahahaha!!!)
→ x⁻⁵ is NOT included in the final answer since we are finding the coefficient

(c) For the constant term x⁰ (which is also the oft-used “term independent of x“), 30 − 5r = 0 ⇒ r = 6
∴ constant term = 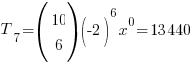$T_7 = (matrix{2}{1}{10 6})(-2)^6 x^0 = 13 440$ (MUAHAHAHAHA!!! :twisted:)
→ we don’t include x⁰ in the final answer since it is a constant

Feels great to be powerful isn’t it? But please don’t write “Muahahaha” on your actual answer script 😛

Tekan Revision Exercise

(i) In the binomial expansion of 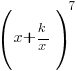, where k is a positive constant, the coefficients of x³ and x are the same. Find the value of k.

(ii) Using the value of k found in part (i), find the coefficient of x⁷ in the expansion of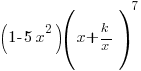

[Answer: k = 3/5, Coefficient of x⁷ = −20]

[+] D. When `n` is Unknown …

Whenever n is unknown, it’s almost certain that you’ll have to expand the ⁿC_r Formula into the 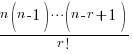form within an expansion or T_r+1 formula (that nCr calculator button will suddenly become useless for those who like to keep pressing it), to obtain the value of n and some other variables via the comparison of the coefficients of suitable terms.

Given that (1 + ax)ⁿ = 1 − 12x + 63x² + …, find a and n.

ANS: (1 + ax)ⁿ = 1ⁿ + ⁿC₁1ⁿ⁻¹(ax) + ⁿC₂1ⁿ⁻²(ax)² + …
→ since there’s only one x term with non-negative power in the expression, we only need to expand to the first 3 terms
= 1 + nax + 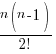a²x² + …
→ instead of trying to derive from the definition of ⁿC_r given in the formula sheet, being familiar with the ⁿC₁ to ⁿC₄ expressions will be handy here.

Compare Coefficients

Comparing our own expansion with the given expansion,

na = −12 —– (1) → compare coefficients of x
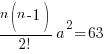${n(n-1)}/{2!}a^2 = 63$ —– (2) → compare coefficients of x²
Sub a = −12/n into (2):
${n(n-1)}/{2}(-12/n)^2 = 63$
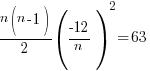
9n = 72
∴ n = 8
Sub n = 72 into (1):
∴ a = −12/8 = 3/2

Tekan Revision Exercise

In the expansion of (2 + 3x)ⁿ, the coefficients of x³ and x⁴ are in the ratio 8 : 15. Find the value of n.

[Answer: n = 8]

[+] Summary Exercise

To round things off, now that you have understood the 4 kinds of binomial questions I’ve just taught you, you should be able to solve (with one of your eyes closed) this question from the 2009 GCE ‘O’ Level AMaths Paper 2 that had somehow resulted in massive outpouring of grief among those who took the paper that year.

(i) Write down the first three terms in the expansion, in ascending powers of x, of 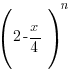, where n is a positive integer greater than 2.

The first two terms in the expansion, in ascending powers of x, of 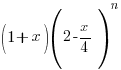are a + bx², where a and b are constants.

(ii) Find the value of n.
(iii) Hence find the value of a and b.

[Answer: n = 8, a = 256, b = −144]

Now make sure you hand in your completed homework the next time I see you or you’ll be surprised at the nasty stuff I can do to you! I’ll be watching you ….

The Justin Bleah Bleah song started playing again, waking him from his slumber.

Realizing that he must have been talking in his sleep again, he wiped away the disgusting saliva that had stained his sleeve, before proceeding to attempt a couple of those depressingly-humorless questions in his binomial notes.

And then he suddenly realized that those questions actually fall into four main types …

頑張って!!!

Sadako Loi