Based on another true story …
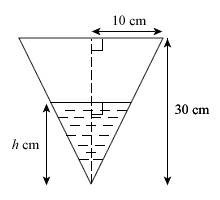
Given that Little Miss Loi’s … umm … bla *water container comes in the form of an inverted cone of height 30 cm and base radius 20 cm, and that the water in the container is rising at a constant rate of 20 cm3s−1.
- Express the volume of water in the container, V, in terms of: π and the depth of water in the container, h.
- If the depth of water is currently at 24 cm, find the rate of increase of h at this very instant.
- Find the number of seconds left for Little Miss Loi to reach the toilet (i.e. when the water container fills up fully and begins to … umm … leak).
*For hypothetical use only.
頑張って!!!
11 Comments
曜
日
Take photo of your own car. take photo of her and her car. then walk away.
曜
日
'cher, why your car flip to the side one?
曜
日
i love how you link random scenarios to math questions. hahaha you're at a much higher level than me. All the way miss loi!
-yourfan
曜
日
Feel like hijacking again.. but 不要啦。Sadako Loi 还没有放过我。
曜
日
Van: Unfortunately, from the field report, it seemed pretty hard to do that with all the intense verbal bombardment going on *BOOMZ*
DC: Such was the power of the Ah Lian's @#$%^* 狮子吼. Quick! Go help Little Miss Loi flip the car back!
chanchinhong: Fan? *shy* *blushes*
mathslover: Unfortunately, as that Plane Geometry question wasn't proved within 7 days, she ended up 阴魂不散 ... and is now roaming around haunting all students studying late nights for the O-Levels 🙁
曜
日
@Sadako Loi: Prove already! Go see and go back to where you belong! 🙁
曜
日
1)Volume of a cone =
To find the radius of the water level:
Therefor :
Miss Loi: Yes part 1 is straightforward. Main thing you'll need to recall is the expression for the volume of a cone that you've been drummed into since your lower-secondary days:
--- (1)
We're given h but not r and thus we'll need to express r in terms of h to obtain the final expression.
To do this, we can make use of the tangent of the common angle (see diagram above) like what Nash has done or we can simply consider the ratios of the two similar triangles i.e.
Sub in this expression of r into (1) and you'll get
--- (2)
2) To find rate of increase of h i.e.
,
→ this step is unsafe!!!
cm/s = 0.0994 cm/s
When h=24,
Alright we're about to enter into a bit of Chain Rule Controversy here.
You've established your Chain Rule expression as
, but you've differentiated V (in (2)) with respect to h and apparently looked to have simply anyhow inverted your 
to obtain your 
to in order to sub into your Chain Rule expression.
While this will not affect your final (correct) answer, it's important to note that terms like
are derivatives NOT fractions. So performing an Olympic-style backflip like this in your working has been known to get on the nerves of some mathematically-edgy teachers who may suspect that you don't actually know what you're doing!
So since we've already established V in terms of h in Part 1, Miss Loi thinks it's safer to express your Chain Rule as:
... and obtain your
(note the use of 
instead of 
)
Or if you wish to use your original expression of
, then it's safer to differentiate h with respect to V (i.e. 
) after first expressing h in terms of V.
3) Total volume=
= 1000π cm3
Note:you should get the same value if you sub h=30 cm into your Part 1 expression i.e.
Volume when h= 24,
= 512π cm3
Time left before err... overflow =
= 76.6s
Part 3 is common-sensical and straightforward, but unfortunately many students keep thinking about "Rate of Change question means must dy/dx!" by the time they reach this stage!
Since the rate of change of volume is constant at 20 cm3s−1, we simply obtain the time to overflow by:
(Vol.overflow (i.e. h=30) − Vol.h=24)/(Rate of change of vol.) = see Nash's workings above 😉
I think its a bit wrong somewhere...
You should have just ignored her nagging and just walk/ sprint to the nearest toilet, not much she can do with your car in the parking lot anyways... unless of course she goes violent and starts scratching, then you can sue her ^_^.
曜
日
Nash: Added a diagram for visibility and marked your working - please pay attention to Miss Loi's notes on Part 2!
Oh and the latest field report from Little Miss Loi was that the Ah Lian's fingernails were Wolverine-like sharp!
And, and ... coz of that, h became ...
*a mysterious force from nowhere violently pushed Miss Loi away from the computer before she could finish typing*
曜
日
Erm... 'cher, the way you set the question, not only "Cheem", but also very wrong leh... You should have done what Nash suggested (You should have just ignored her nagging and just walk/ sprint to the nearest toilet, not much she can do with your car in the parking lot anyways… unless of course she goes violent and starts scratching, then you can sue her ^_^.)
曜
日
Alright, alright ... can we assume that, as the car was loaned to Little Miss Loi (Note it's Little Miss Loi, not Miss Loi), her supreme sense of responsibility to the car far, far outweighs her need to visit the toilet - at least not till the very last minute.
Besides, suing people costs a lot of time, karma and $$$!
曜
日
Ok part (2) noted...
The story-sum questions you post are more refreshing than the traditional questions in papers and made me intrested in maths again. Thanks alot!
Lesson learnt:
1) Don't irritate mathematically edgy teachers with half-baked maths statements
2) Value your car before dignity
3) Carry a pepper-spray (in case of ah lians with claws instead of hands)
4) Go to the toilet BEFORE driving
5) The phrase "-BOOMZ-" has changed from mockery to a cool statement? Ridiculous =_=...