THE CLOCK STRIKES TWELVE
Voting for the S’pore Blog Awards has closed.
Miss Loi is eternally grateful to all who had supported Jφss Sticks throughout this grueling voting marathon. It’s up to the judges now.
Like a Dark Damsel in her black dress, Miss Loi hopped onto her Black Mobile as soon as the last Jφss Sticks session ended.
The clock ticked down as she burst out of her Novena underground carpark in a flash, and sped towards a gloomy Vivo City on a dark Monday night, narrowly escaping a number of villainous ERPs along the way.
But arrived she did, albeit being ambushed by another ERP inside the City.
In an exceptionally brave move, The Dark Damsel passed under that ERP without a Cashcard, and hurried up the empty stairs to enter a hall in the nick of time for a showdown with … umm … these Jokers
Alrighty, as a S’pore Blog Awards finalist, The Dark Damsel Miss Loi was kindly invited by Omy.sg to the Gala Premiere of Money No Enough 2.
Without giving the plot away, Miss Loi thinks that the movie flows well and, in typical Jack Neo fashion, should have no problem finding its identity with most Singaporeans (esp. in the scene where something was thrown into the sea) – though the hardcore use of Hokkien as Singapore’s national language might be a little problematic for non-native Hokkien speakers.
Also, special mention must be made of the Ah Ma actress who, like Heath Ledger in The Dark Knight, gave an absolutely outstanding and thoroughly memorable performance to embody the “Poorer than Poor” message that the film tries to send out.

But whatever novelty of attending this premiere screening was negated by the fact that Miss Loi is now nursing a terrible neck ache after staring at hugely deformed faces of Jack Neo, Mark Lee and 辉哥 for over two hours.
You see, being an invited event, it was free sitting in the cinema.
And having to rush down at the last minute meant that Miss Loi was relegated to the second row from the front by all the kiasu Singaporeans who managed to fill more seats than they physically could with their bags, newspapers, books, babies etc.
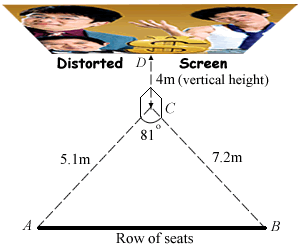
ABC is a triangle on the horizontal plane with AB being the row of seats that Miss Loi was sitting at.
CD is the vertical height from the floor to the screen.
Calculate
- The length of the row of seats AB.
- The area of the triangular area ABC.
- The angle of elevation of the screen as seen from A.
- The angle of elevation of the screen as seen from B.
- The largest angle of elevation of the screen that can be seen along AB.
Hence deduce (based on the angle of elevation alone) where Miss Loi sat on Monday night, and where was the worst seat that she could have sat in that row 😉
Obviously, common sense will give you the answer but since the word HENCE has appeared, you have no choice but to 乖乖 calculate the answers like a Sec 3 E-Maths student 😉
Some info regarding angles of elevation/depression (amongst other things) can be found at the end of this dramatic blog post. So everyone should be able to locate Miss Loi now, especially since this is a standard O-Level TYS question!
Oh and there’re just TWO MORE DAYS before voting ends!
Miss Loi thanks everyone for your support from the bottom of her heart *Takes a deep bow – Ouch – neck pain!*
The finishing line is within sight – just TWO MORE VOTES (one by tonight & one more tomorrow) from each of you and it’ll be over.
Please don’t let Miss Loi end up with Votes No Enough! Can??? Pleeease??? …. *shows 水汪汪的眼睛*







 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 





















17 Comments
曜
日
Hey Miss Loi!
I was initially up front but my mum couldn't tahan the view so we shifted to the back in seprate seats...
Which one was you?
Now that you've mentioned, I'm going to include the kiasu people... 🙂
Thanks.
曜
日
1. 8.14m
2. 54.4 m^2
3. 38.1 degrees
4. 29.1 degrees
5. 16.7 degrees
The solution is here
http://base.googlehosted.com/base_media?q=hand-8176000598797796082&size=1
曜
日
*shakes head* only you can come out with questions for daily life. hahaha.. no wonder you're the best math High Priestess cum blogger. 😛
曜
日
@Samantha> She was the one with the stiff neck after the show.
WAHAHAHAHAHAHAHA!!!!
曜
日
You were at the Gala Premier!? oi... never give a holler!
Voted. All the best. Lucky I bring assistants to chope seats while I go photo taking.
曜
日
Samantha: So poor thing that your Mom & you ended up separated by newspapers, bags and babies.
One look at the diagram and should tell you where Miss Loi was - think she saw you that night too 😉
Soupie: *shakes head - ouch!*
Krisandro: -_-
ECL: Were you at Hall 3? If so, didn't you see a Last-Minute Buddha Foot Hugging tutor staggering into the cinema just before Jack & Co appeared?
Lucky you - Miss Loi's 'assistant' FAILED!
曜
日
1. By cosine law, AB2 = 5.12 + 7.22 - 2(5.1)(7.2)cos81°
AB = 8.15m (3 sig fig)
Yeah no sweat - Cosine Rule rulez!
2. By Heron's formula,

Area of ABC =
= 18.1m2 (3 sig fig)
Interesting that you've used Heron's Formula for this part.
But for Singapore's Sec 3 E-Maths students, most should find it slightly more straightforward to sub in the values directly into the alternate area of triangle formula:
Area =
= 0.5(AC)(BC)sin81°
= 0.5(5.1)(7.2)sin81°
= 18.1m2
3. angle of elevation from A = = 38.1° (3 sig fig)
= 38.1° (3 sig fig)
Nothing like a good diagram to illustrate how you get θ the angle of elevation 😉
4. angle of elevation from B = = 29.1° (3 sig fig)
= 29.1° (3 sig fig)
Ditto as with Part 3 😉
5. The largest angle of elevation is the angle between ABC and ABD. Let the altitude of ABC from C be x m.
Yes whenever you're asked to calculate "the largest angle of elevation" of (in this case) D as seen from a point along AB, it's IMPORTANT to know that this occurs at the point (let's call it E) with the the shortest distance from D (which is the distance x in your working.
Somehow, many students still tend to forget this in the heat of their exams *sigh*
Area of ABC =

x =
Of course, x happens to be the height of Δ ABC.
So having already obtained the length of AB in Part 1, and area of Δ ABC earlier in Part 2:
18.1 = 0.5(AB)x = (0.5)(8.15)x
⇒ x = 4.44m
*Do note that multi-part questions are often designed to let you 're-use' answers in earlier parts to save you time in recalculating everything, or you can take these as opportunities to 'double-check' your earlier answers if you're the 'not confident' type 😛
.'. The required angle = = 41.9° (3 sig fig)
= 41.9° (3 sig fig)
So using the x you've calculated, you'll find the max neck-breaking angle of elevation to be 42°!!!
You saw distorted faces. So you were most likely sitting at A, where you needed to raise your head higher.
The distance from the base of the altitude of ABC from C to A is , i.e. 2.49m from A. So the worst seat you could have sat on would be 2.49m from A.
, i.e. 2.49m from A. So the worst seat you could have sat on would be 2.49m from A.
若有紕漏,不吝賜教!
You sure did get the worst seats right but since the answer should be based solely on the angles of elevation:
∠ of elevation from A = 38.1°
∠ of elevation from B = 29.1°
And since Miss Loi is not a particularly tall person, why should be she be sitting at A????
曜
日
I especially like these calculator questions in HK's Mathematics and Additional Mathematics exam papers. 😉
Oh and I find that someone who 捷足先登 made a mistake.
曜
日
It seems I made an error calculating something. =(
曜
日
Li-sa: See Miss Loi's comments on your workings 😉
Someone: Your error is in Part 2 (area of the Δ ABC) but your working's fine so it could be down to pushing the wrong buttons in your calculator.
As you can see, in a multi-part question, an error in an earlier part can easily snowball into errors in later part of the question (i.e. Part 5) so please tread with care!
Though it's probably not related to your case, Miss Loi would like to take this opportunity to remind all students to make sure your calculator is set to DEGREE MODE (vs RADIAN) to avoid a repeat of the tragedies that have been afflicting many students.
Do you know then, which kind of questions would require you to express your angles in RADIANS (e.g. π, π/2 etc.)?
And a nice touch for the TOA CAH SOH parts in your workings and for this question we can safely assume that the angles of elevation will never exceed 90°, else the screen will be on top and over everyone's head!
This is not an Omnimax theatre! LOL
曜
日
Hmm ... I've got the feeling we were sitting in the same row
曜
日
Yeah, I pressed the buttons wrongly. So embarrassing. Haha.
曜
日
rinaz: A fellow Row 2-er? Ain't the view fantastic that night?
Oh, and
Happy Birthday Gal!
And Someone, there's absolutely nothing to be embarrassed about. As the old adage goes: "It's better to have tried and pressed the calculator buttons wrongly then never tried at all"! 😉
曜
日
So is the worst seat possible at A? Seems that the angles of elevation also include the greatest one of 42 degrees. Does that mean if one is not allowed to find the distance between foot of x and A then the angle can't be used?
.l
曜
日
.I: The angle of elevation is the angle above horizontal from a point X looking upwards towards another point Y that is higher. (What about the angle of depression then? 🙂 )
So in our case we have 3 lower points A, B and E (from the workings in comment #7) looking upwards towards a common point D.
However each of the points A, B and E has a different angle of elevation as their respective distances from D (or C) is different.
So to summarize once more the angles of elevations obtained from the workings in Comment#7:
∠ of elevation from A = 38.1°
∠ of elevation from B = 29.1°
∠ of elevation from E = 42°
One can safely assume that these angles are the max/min values since all other points between A & E & B would have angles that are < 42° and > 29.1°
Where would you rather sit if you want your neck to bend upwards the least?
Which is the worst spot where your neck needs to bend upwards the most?
P.S. Not sure if Miss Loi understood the 2nd part of your question, but if you know your TOA CAH SOH the angle can still be found if you know the distance from AB to D (the hypotenuse) - but this will of course depend on what's given in the question.
曜
日
I KNOW!
radian mode is when calculating arc length and area of sector (when using s= r x θ for arc length and a= r2 x θ/2 for area of sector)
also for A Maths questions when range is given in terms of pi.
Degrees mode for everything else.
Am I right?
曜
日
Correcto Clarion! Steady Poon Pi Pi!!!
Since Circular Measure has now made its way into the New Syllabus, E-Maths students now have to be careful to express your angle θ to RADIAN in your arc length and sector area formulae.
On top of that, A-Maths students must remember to do likewise whenever you see range of angles like 0 < x < 2π in any of your trigonometry questions!