Continuing from the previous episode …
Months later, in a tension-filled room …
This is the information they managed to extract from the Maths Tutor’s feisty aunty, before they got chased off by her reinforcement aunties via an intense attack of umbrellas, shoes, handbags etc. …
For some superstitious reason, the Maths Tutor had chosen The Temple to be located at a postal code based on a sequence with its first five terms T1, T2, T3, T4, T5 as follows:
T1 = 1 = 1
T2 = 3 = 1 + 2
T3 = 6 = 1 + 2 + 3
T4 = 10 = 1 + 2 + 3 + 4
T5 = 15 = 1 + 2 + 3 + 4 + 5
The nth term in the sequence is given by
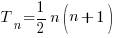
Find T350 and hence find The Temple‘s postal code which is the solution of
5 + 10 + 15 + … + 1750.
Even though most of them failed their PSLE math, this should really, really be a simple one.

 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 





















9 Comments
曜
日
T350= 1+2+3+4+...+349+350
=(1+350)+(2+349)+(3+348)+...
=351x (350/2)
=61425
(Sum of AP, just using non-A Level stuff to solve.)
5+10+15+...+1750=5(1+2+3+4...+350)
=5x61425
=307125
曜
日
I just realised you gave the sum of AP formula but I didn't use. D:
曜
日
Hi Miss Loi..nice AP question
Sorry i can't impress you with nice mathematical equations, i am simply too lazy.
Using primary school rudimentary method:
First time plus last term : 5 + 1750 = 1755
Number of terms: ((1750-5) / 5) + 1 = 350
Total sum:( 350 X 1755) / 2 = 307 125
Using frantically pressing of P 6 calculator : 307 125
(Or) a smart way to use TI-84 Plus: 307 125
A level method:
1st term: 5
last term: 1750
d = 2
n = 350
Sn = 350 /2 ( 2 (5) + ( 350 - 1)( 5) ) = 350/2 (5 + 1750)
= 307 125
AP is so fun =)
Pity those people that are sabotaged by SEAB years ago by this equation
1 + 2 + 3 + 4 + ...+ 99 + 100
曜
日
"Sir, that postal code doesn't exist. Your intelligence failed." -- the henchman.
曜
日
@mathslover: Oh the feisty aunty was loyal to the Maths Tutor till the very end.
曜
日
Aiyo the A-Level A.P/G.P. folks (armed with super duper TI-84 Plus calculators) seem to have invaded this turf ...
But for EMaths students without such heavy armament, Number Patterns, like its Plane Geometry counterpart in AMaths, usually requires a little 阴阳眼 prowess in order to 'see' the pattern and unravel the Da Vinci Code-styled number sequences, though there are certain standard formulae for common sequences.
In this case there are many ways to get the simple answer, as described by clarion and TJK, but some students will have the tendency to stare at the sequence for a long, long time and wonder how on earth to 'minus every 1st-4th terms from each set of five terms' (or whatever) to obtain your 5+10+15+...+1750.
In times like these, if you ever find yourself going deeper and deeper into a pit in the midst of your exam, it's always good to prevent a 走火入魔 situation by either
1) revisit this part later (esp if it carries little marks) or
2) take a deep breath, look up to the heavens, invoke the changing your point of view strategy described in your textbook OPEN your eyes, like clarion with his 阴阳眼 has done to get:
5 + 10 + 15 + ... + 1750
= 5(1 + 2 + 3 + ... + 350)
= 5[(0.5)(350)(350+1)] = 307125
Note: This is a hence question so you must use T350 to obtain the final answer.
So sweet, so simple - even the Ah Beng's primary school-educated henchmen should have no problem with this (without the need for frantic pressing of calculators) ... such is simplicity of most Number Patterns questions, since afterall it's a Sec One topic!
曜
日
Hi Miss Loi,
in the end part (0.5)(350)(350 +1) also uses AP concept mah....
now i appreciate the power of the GC (shielding power), in the past i am worried once such question approaches me like a devil.
I still remembered the days where parents lamented SEAB for this PSLE question
1+ 2+3+4+ ...+100
Nice olden days
曜
日
350th term: 0.5*350*(350+1)
=61425
Therefore, the postal code is..........
61425*5=307125, as 1750 divided by 5 is 350. Thus, (350th term)*5=postal code!
So smart of me!!!!
曜
日
LOL A Hitler rant parody yay!