noise pollution in Miss Loi’s estate at 2am
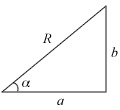
Like Honda’s Type R variant of cars that appeal to Ah Beng racer boys who like to bully weave in front of Miss Loi’s demure little car on the expressways, Trigonometry has its own “Type R” model in the form of the R-Formula that was unveiled in this year’s New AMaths Syllabus.
As such students are warned to listen out for the roar of the R-Formula whenever you encounter a trigonometric question:
with an expression that contains a constant, like this:
Solve for 0° < x < 360°,
2 cot x = 3 + 2 cosec xor where you’re asked to find an expression’s max/min value, like in this rather cheong hei (long-winded) question:
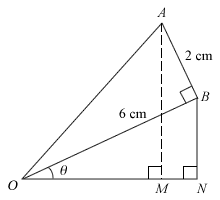
The diagram shows two right-angled triangles with their right angles at B and N. The sides OB and AB are of length 6 cm and 2 cm respectively. The lines OB is inclined at angle θ to ON. The line AM is perpendicular to ON.
- Express OM in the form OM = R cos (θ + α) and calculate the values of R and α.
- Find the value of θ for which OM = 5 cm.
- In the diagram, state the line with a length of R cm and the angle with a value α.
- Express AM in terms of R and (θ + α) and show that the area of triangle OAM is 10 sin 2(θ + α).
- Given that θ can vary, find the maximum value of the area of triangle OAM and the corresponding value of θ when this occurs.
To handle the new R-Formula questions, students need to recall the following expressions, as they will not be appearing on your formula sheet during your actual exam:
The R-Formula
- a cos θ ± b sin θ = R cos (θ ∓ α) – look out for that inverted plus/minus!
- a sin θ ± b cos θ = R sin (θ ± α)
where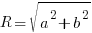 
and 
and 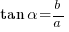a > 0, b > 0, α is acute
Maximum/Minimum Values of R-Formula Expressions
- The maximum value is R which occurs when cos/sin (θ ± α) = 1
- the minimum value –R which occurs when cos/sin (θ ± α) = -1
Deriving The R-Formula
Do note that the R-Formula highlighted above is NOT a given, especially when the relevant part of the question carries a high weightage of marks e.g.
There’s a bit of debate on this but don’t think you can get away with all 6 marks here by simply substituting the values into the R-Formula! So to be a little kiasu, it’s advisable to derive the whole thing as per the following steps:
4 cos θ – 3 sin θ
= R cos (θ+α)
= R [cosθcosα-sinθsinα] (Addition Formula)
= (R cosα)cosθ-(R sinα)sinθ
Comparing coefficients between LHS & RHS,
R cosα = 4 —– (1)
R sinα = 3 —– (2)
(2)/(1): tan α = 3/4 ⇒ α = 36.9°
(1)2+(2)2:
R2cos2α+R2sin2α = 42+32
R2[cos2α+sin2α] = 25 ⇒ R = 5
∴ 4 cos θ – 3 sin θ = 5 cos(θ+36.9°)
Important Notes
To reiterate what was stated above, a and b MUST be positive. DON’T do this:
(-3) cos θ + (-2) sin θ = 3 → WRONG!
Instead, move the terms around to ensure that the first term is always positive:
3 cos θ + 2 sin θ = -3 → CORRECT! YAY!
Please, please, please, please, please for the addition cases (i.e. a cos θ + b sin θ or a sin θ + b cos θ) you can simply re-arrange the sine and cosine terms depending on how you wish to express the R function in your question.
E.g.
3 cos θ + 2 sin θ → if you require R cos (θ – α)
2 sin θ + 3 cos θ → if you require R sin (θ + α)
Hailed as the pinnacle of O-Level Trigonometry, a typical R-Formula question may also require your skills on lesser trigonometry variants such as the Addition Formulae, or the Double Angle Formulae, or the Factor Formulae, together with your knowledge of basic angles (e.g. in question 1 above when you’re asked to find all angles within the range of blah blah blah).
But once you tame it, you’ll be rewarded with a straightforward ride and zoom away with plenty of marks.
So are you ready to test-drive your R-Formula with the two questions above? Miss Loi doesn’t expect you to crash this in your O-Level in two weeks’ time!
*Zooms away for Jφss Sticks Sessions (Type-R variant)*
N.B. Once again, Miss Loi does NOT advocate nor encourage speeding or any form of street racing in Singapore.
24 Comments
曜
日
I'm trying this for fun =) (for lbmfh practice actually)
Miss Loi is now marking your answer in a LMBFH manner too 😛 ...
1)Is there only 1 answer? My only answer is 247.4
Yes you're right there's only one answer! To elaborate, we have
2 cot x = 3 + 2 cosec x
So seeing that lonely constant 3 in the equation should signal to you that you're going to start the Trigonometry R-Formula engine *VRROOOOOM*
Expanding ...
(Note: we put the [2 cos x] as the first term so as to keep a (in the R-Formula) positive)
To express the LHS above in R cos (x + α) form, we have
R = √(22+32) = √13
tan α = 3/2 ⇒ α = 56.3°
(Note: Both a & b has to be > 0 when you're obtaining α! DON'T do a tan α = -3/2!)
So we now have:
√13 cos (x + 56.3°) = 2
⇒ cos (x + 56.3°) = 2/√13
This is where many students get pwned and forget that All Science Teachers are Crazy (ASTC), as the question asks for ALL values of x in the range of 0° < x < 360°.
So doing a cos-1 2/√13 in your calculator will only yield a basic angle of (x + 56.3°) = 56.3°. But since 2/√13 is positive, we see from the ASTC diagram below that:
⇒ x + 56.3° = 56.3°, 303.7° (1st and 4th quadrant)
⇒ x = 0°, 247.4°
But we shall take only x = 247.4° since 0° is not in the range of 0° < x < 360°!
2)(i)√40cos(θ+18.43)
Once again, to elaborate on your answer (next time show workings okay? Tsk tsk.) ...
Typically in a question like this, we first need to express OM in terms of sin θ and cos θ BEFORE we can use the R-Formula. From the following diagram,
... you should be able to see that ∠MAB = θ, and since OM = ON - MN
⇒ OM = 6 cos θ - 2 sin θ
(using your TOA CAH SOH)
Using the R-Formula,
OM = R cos (θ + α) ----- (1)
R = √(62+22) = √40
α = tan-1 2/6 = 18.435°
⇒ OM = √40 cos (θ + 18.435°)
(ii)56.2
Think you've made a careless mistake here but Miss Loi won't know in her lifetime the cause of it since your workings are absent!
In anycase, simply equate OM to 5cm and find the value of θ when this occurs:
√40 cos (θ + 18.435°) = 5
cos (θ + 18.4°) = 5/√40
(θ + 18.435°) = 37.761°, 322.239°
Once again don't forget to A-S-T-C thingy BUT BUT BUT in this case we're sure from the diagram that θ is acute so we can safely discard the 322.239° and conclude that:
θ = 37.761° - 18.435° = 19.3° when OM = 5cm
(iii)AO, angle AOB
This part requires a bit of 阴阳眼 (The Third Eye) which Anoneemers has demonstrated that he obviously possesses one 😉
You should be able to 'see' this from the diagram above 😉
(iv)AM=Rsin(θ + α)=√40sin(θ+18.43)
Area of OAM
=(0.5)[√40sin(θ+18.43)][√40cos(θ+18.43)
=20sin(θ+18.43)cos(θ+18.43)
=10sin 2(θ+18.43)
WOAH you have workings now! Yes, from the diagram in Part iii., you can easily see that
AM = R sin (θ+α) ----- (2) simple right???
But if you read carefully again, Part iv. only requires you to express in terms of R and (θ+α) (vs Part i. which required you to calculate the values of R and α). So strictly speaking you shouldn't replace R and α with their actual values in your answer at this point.
Now area of ΔOAM = 0.5 x OM x AM. Using the expressions in (1) and (2),
Area of ΔOAM
= 0.5 x R cos (θ + α) x R sin (θ+α)
= (0.5)R2(0.5) 2 cos (θ + α) sin (θ+α)
(when you see a sine and cosine term with the same angle together - you should instinctively think of the Double Angle Formula for sine!)
Sub in R = √40 obtained from Part i.
= (√402/4) sin 2(θ + α)
= 10 sin 2(θ + α) YAY!
(v)10
Marks are usually served to you on the platter in the Maximum/Minimum parts of R-Formula questions so DON'T EVER 对不起你自己 and skip this part!
From the notes above: The maximum value is R which occurs when cos/sin (θ ± α) = 1.
So in our case the maximum area is simple 10 cm2 (the coefficient of our expression in Part iv) and this occurs when sin 2(θ + α) = 1
⇒ sin 2(θ + 18.435°) = 1
⇒ 2(θ + 18.435°) = 90°
⇒ θ = 26.6° (since θ must be acute)
By the way how do u type all those square roots and teeter symbol i had to copy and paste =.=
It's my 1st time making
曜
日
Hey Anoneemers, Miss Loi has commented on your test drive of the Trigo R-Formula questions.
Regarding the symbols, Miss Loi was taught from the start to reference this table. But after awhile it became pretty intuitive e.g. for α you type α, for β you type β etc.
But having said that, copy and pasting still seem to be the quickest!
曜
日
What? This thing is in O level A maths nowadays? We're moving closer to this day...
Used to take a long time remembering this when I did A levels, and until now still cannot figure out the logic behind all those steps used to derive the Rsin and Rcos.
曜
日
mathslover: As far as Miss Loi can recall (please correct if she's wrong though), the R-formula was only removed from the A-Math syllabus between 2002-2007, as she could still remember herself utilizing the R-Formula diligently when she was still a kawaii teeny Sec Four school girl.
So her kaypoh guess is you're around 18-23 yrs-old? Oh wait ... but you know how to do Plane Geometry questions!
The plot thickens ...
曜
日
Miss Loi: Actually, my O level year not within the range.
Its the extraordinary year where matrices and vectors are out.Guess either u remember wrongly, or i was sleeping in A maths class..
Plane Geometry is new? I kinda faintly remembered doing something called Circular Measure which include tangent/chord/segment/sector...
No plot lah Miss Loi, you
watch too much HK dramaput your kawaii notes below the prawns so big, anyone can do the question le. 🙂曜
日
Help! I can't get the answer for this question, 4sin3x + 3cos3x=√3.
Tried doing the question for 2-3 times but still can't get the answer.
I don't understand the minimum and maximum thing 🙁 🙁
曜
日
Hello Rose, yours is really a classic a sin θ ± b cos θ = c trigonometric equation question.
First understand that the R-Formula part i.e. converting the LHS into a R-Formula expression, is straightforward:
Sub a=4, b=3 for *R sin (θ±α) (do check with your Cher if you need to derive the R-Formula using Addition Formula, especially if the part carries a lot of marks),
R = √(a2+b2) = √(42+32) = 5
α = tan−1
= tan−1
≈ 36.870°
Thus your LHS: 4 sin 3x + 3 cos 3x can be expressed as:
5 sin (3x + 36.870°)
To address your confusion of the "minimum and maximum thing", as Miss Loi has no further detail of your question, let's assume that we're looking for the max/min values of 5 sin (3x + 36.870°).
Consider the typical graph of a sine function y = a sin θ which you learnt in Sec 3:
Looking at your R-Formula expression of 5 sin (3x + 36.870°), can you see that it's also a sine graph when you let a=5 and θ = 3x+36.870°? Hence from the diagram above, the max value is 5 and the min value is −5.
Now to solve for x in your equation (the part where many students get KIA because they often forget about their basic angles):
We have:
5 sin (3x + 36.870°) = √3
sin (3x + 36.870°) =
Basic angle β = sin−1
= 20.268°
Assuming your question asks for all values of x in the range 0° ≤ x ≤ 360°,
Since sin (3x + 36.870°) is positive,
⇒ 3x + 36.870°
= 20.268°, 159.732°, 380.268°, 519.732°, 740.268°, 879.732°
Note that since it's 3x in the expression, we need to go 3 rounds round the SATC diagram i.e. β + 0°, β + 360°, β + 720°
3x = −16.602°, 122.862°, 343.398°, 482.862°, 703.398°, 842.862°
∴ x ≈ 354.5°, 50.0°, 114.5°, 161.0°, 234.5°, 281.0°
Does the answer tally with yours?
曜
日
Thank you!
Erm... Can you teach me how to find the max and min values of (5sinx - 12cosx)²?
曜
日
Hello again Rose and a interesting but nonetheless a pretty straightforward question you have!
To find the max/min values of (5 sin x − 12 cos x)², you may first express the expression within the brackets using the R-Formula i.e:
(5 sin x − 12 cos x)² = [R sin (x − α)]²
As discussed earlier throughout this blog post,
we know R = √(5²+12²) = 13
⇒ (5 sin x − 12 cos x)² = [13 sin (x − α)]²
Since max/min value of sin (x − α) = ±1, we can deduce that the max/min value of 5 sin x − 12 cos x = ±13 BUT we're dealing with a SQUARED expression (5 sin x − 12 cos x)² so
Max value = 13² = 169
Min value = 0 (since the square of a −ve term is always +ve)
Happy New Year!
曜
日
I am weak in trigonometry, and realise that it stands a huge amount of marks in paper 2. I'm a Sec 4 student and MYE is coming :S
曜
日
@AMath Student: Yes for e.g. in the TYS's analysis of the 2008 GCE 'O' Level AMaths paper, Trigonometry (Trigo functions, identities & equations, R-formula etc.) took up a whooping 39 marks (21.6%) of the total marks across Papers 1 and 2.
This is second only to calculus i.e. Differentiation & Integration (45 marks/25%) which incidentally also contains trigonometric functions 😉
Good luck for your Mids! Take this as a good practice opportunity for almost 90% of your O Level topics - though Miss Loi can't wait for them to end at the moment 😕
曜
日
i m weak in math s ive an exam on 1 june please guide me wat can id o to get a seat in bitsat
曜
日
Miss Loi is teta = 90°- alpha in the first triangle?
曜
日
sorry I was referring to the second diagram I didnot see the first one?
曜
日
@Jukie Primestein: Are you referring to this diagram?
If so, you'll find in ΔOAB from the diagram above that θ < 90° − α
曜
日
Can you please send me a few more variation of the roar R-formula. Based on a few times I encountered it it is not always clear if you are to find a maximum or minimum! Oh another question I have not seen any proof to convince me than cosine of a negative number is positive, but please don't get me wrong I know it is correct however a proof maybe through a diagram would really do the trick!
曜
日
which trig identity do you refer to as the factor formula?
曜
日
@Jukie Primestein: If Miss Loi gets your question right ... the Factor Formulae refer to
Are they called the same thing over at Reggae Jamaica? 😉
曜
日
why cannot r be negative 5 in the exaple given ?
曜
日
Hi Miss Loi,
I love your site and your sense of humour, definitely very localised.
Anyway, a quick question to your type-R question 2, the part on maximum area of the triangle.
Should we apply the maximum value of R at the length stage? meaning to AM and OM individually instead of applying to the area straghit?
The maximum value of AM and OM exist when cos (θ + α) =1, Hence, maximum value for AM and OM should be √40. Hence, 1/2 times AM times OM should give us 20cm sq.?
I'm confused. Pls clarify if you can? Thanks! =]
曜
日
@Ray: Hello and welcome to Jφss Sticks, Ray!
From parts 2(i) & 2(iii) of the workings here,
OM = √40 cos (θ+18.43°)
AM = √40 sin (θ+18.43°)
This means that both the lengths of OM and AM are dependent on the same angle θ, which, looking at the equations above, means that both cannot be maximum at the same value of θ
i.e. When OM is maximized when cos (θ + α) = 1, AM is actually minimized at this same value of θ since sin (θ + α) = 0.
So the key here is we need an intermediate value of θ that will maximize the area instead of the individual lengths hence we have to obtain the ONE R-formula for the area using the double-angle formula etc.
曜
日
Hi. I was wondering if you can help me with these questions.
8 cos x - 15 sin x = 17 cos (x + 1.08) -------- (R formula)
1. Find the minimum and maximum value of 20 - 8 cos x + 15 sin x and the corresponding x values for 0 ≤ x ≤ 2π.
2. Solve the equation |8 cos x - 15 sin x| = 6 for 0 ≤ x ≤ 2π.
Thanks in advance!
曜
日
@Agnes: Look ma! A math question in the comments section! ^^
So you have the R-formula
And from the notes above, the maximum/minimum value of a R-formula is ±R so
At this juncture, there'll be a insatiable urge to flip the centre term and make the careless mistake of flipping the inequality signs, +20 on both sides to get what you want i.e.
(✘)
Not only does the above don't make any mathematical sense (3 ≥ x ≥ 37!), one has to always consider the nature of the graph you're dealing with when it comes to inequalities. From your Trigonometric Equations & Graphs, you know that the max/min values of a A cos x curve is still ±A, even when you flip it around for −A cos θ, as shown:
So you may now 安安心心 proceed in a as follows:
∴ Maximum value of 37 occurs when
and minimum value of 3 occurs when
Note: x = −1.08 rejected ∵ 0 ≤ x ≤ 2π
曜
日
@Agnes: For the second part, we simply expand the modulus function as follows
Using the SATC quadrants, we have for cos−1 (6/17):
and for cos−1 (−6/17)