
Many years ago, having heard of its mighty powers in healing a terrifying disease, a cutie pie schoolgirl sought out a Temple in Novena, together with her schoolmates.
Upon discovering that the High Priestess of this temple also possessed the ability to foretell the future, they burst into an uncontrollable delirium of giggles, as teenage girls tend to do, regardless of whether they’re really cute or not.
And so after being cajoled by her bunch of bitchy-looking Eurasian schoolmates, the schoolgirl entered the temple to stand alone before its ultra-sexy High Priestess.
“How will my future partner be?” she asked the High Priestess.
Lei gor mei loy lam yan wui ho leng chai.
Lei yun fan wui sam yuet sup sei hou yat dim mmm sup gao fen dou.
replied the High Priestess in Cantonese, which was loosely translated as
“Your future man very the handsome, and you will find your fate on March 14 at exactly 1.59pm.”
With that, the High Priestess shoved a folded piece of paper into her hand, telling her not to open it till she had found The One on a March 14th , else she would remain a spinster all her life and die horrible deaths in all her future maths tests forever ever after.
Fast forward to the present (March 14 to be exact), this cutie pie schoolgirl was waiting in one of those never ending queues in one of Singapore’s world-class bus interchanges when she caught a glimpse of a gorgeous hunk standing just a couple of places ahead of her.
Like the sunshine which had lifted the gloomy weather in the past days, her face brightened as she slowly surveyed his long flowing hair that resembled infinite tangent curves, and his well-chiseled face that resembled some n-sided polygon.
Her heart skipped a beat when she spotted the cool π tattoo on his shoulder, and that he was holding a file containing the same set of exam papers as hers.
The moment of realization was complete when her watch showed 1.59pm, and 26 seconds.
Unfolding frantically the tattered piece of paper that she had kept all these years, she saw the following …
An old Pi Day tradition allows a woman to make the first move in a romance, provided that she manages to touch a man’s π-spot at exactly 1.59pm, and the man shall turn irrational enough to accept her.
The vicinity of a man’s π-spot can be found by solving the problem below, with O being the location of his heart.
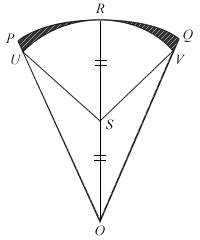
In the figure, the sector OPQ has centre O and radius 6 cm and ∠POQ = 36o. OR bisects ∠POQ and S is the midpoint of OR. An arc, centre S and radius 3 cm is drawn to meet OP and OQ at U and V respectively.
- Find, in terms of π,
- the length of arc PRQ.
- the area of sector OPQ.
- the size of ∠OSU.
- Find the area of the shaded region PRQVU correct to 3 significant figures.
As our love-struck cutie π schoolgirl has not taken A-Maths before, and that Circular Measure has just invaded the Mensuration chapter of the new E-Maths Syllabus, can you help her find the hunk’s π-spot?
There’re not many seconds left before 2.00pm!
Multi-part cheong hei aka long-winded questions like this can often catch out weary students during exams. For they ought to know that:
The length of an arc, s = rθ,
and that the area of a sector, A = 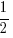 r2θ,
r2θ,
and that θ must always be in radians,
and that π radians = 180o,
and not forgetting something that Miss Loi has already highlighted before here, amongst other things.
The situation is not helped when sadistic examiners sometimes ‘conveniently’ forget to include in the diagram (maybe they’re drawn by someone else?) certain information described in the question. Please save yourself from a major eyeballing exercise by writing down the information on the diagram as soon as you see it!
P.S. This is supposed to be the Pi Day post on 14 March, but Miss Loi has been busily choking on intensive joss sticks smoke this whole week.
P.P.S. Please no naughty comments concerning this π-spot! Yes HAM, Miss Loi’s referring to you!!!!



 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 





















10 Comments
曜
日
Whoa really got Pi day ah..lol..n nice use of the link to the leap day tradition...

曜
日
Aiyoh Soup what kind of indices expression is that? *blushes*
曜
日
Liddat also can! !! So was this your love story?
曜
日
HighwayBlogger, if only it was THIS easy ... tattoo shops' business will skyrocket the week before every March 14 (just like the florists on Feb 14),
and guys will be sitting around everywhere waiting for the ... ummm ... 'poke'*sorry that doesn't sound right*And SDU would've gone extinct much earlier!
曜
日
Ehhhhh!!!! What notty commrnt arrrr??? This Pie tattoo got notty spot meh??? Where arrrr???
曜
日
Easy there HAM ... easy ... it's just an innocent π!
曜
日
Hm..left unsolved for half yr...
* Our cutie π schoolgirl bemoans half a year of wasted youth :'( *
It's always a good first thing to include all values in the question in the diagram, as you may be able to see things that sometimes others can't see *hair stands on neck*
1.i.
Angle POQ = 36π/180 = 0.2π rad
(Yup - just wish to reiterate once more that 180° = π radians NOT 2π!)
Arc PRQ = PO x 0.2π = 6 x 0.2π = 1.2π cm
(Yup - simple substitution into arc length formula s = rθ, with radius r = 6 cm and θ = 0.2π)
ii.Area of sector OPQ = ½(6^2)(0.2π) = 3.6π cm2 , with radius r = 6 cm and θ = 0.2π)
, with radius r = 6 cm and θ = 0.2π)
(simple substitution into sector area formula formula
No sweat so far right? Remember again that all the θ in your arc and sector area formulae must be in radians i.e. in terms of π and/or switch your calculators into RAD mode.
iii.Angle SOU = Angle SOV = 0.2π/2 = 0.1π rad
Angle OSU = π (ie 180 °) - (2x0.1π) = π - 0.2π
= 0.8π rad
Part 2 coming up later...
Yalor as seen from the diagram and described in part 2 of your workings below, since:
So OS = US
⇒ Δ USO is isosceles
⇒ ∠ SUO = ∠ SOU = 18°
⇒ ∠ OSU = 180° - 18° - 18° = 144° = 0.8π rad
See your next comment below for an alternate approach ...
曜
日
Full correction to 1iii.
SU = SR (radii, centre S)
= OS (S midpt of radius OR) = 6/2 = 3cm
Since SU = OS, triangle OSU is isosceles and thus
angle SUO = angle SOU = angle POQ/2
= 0.2π/2 = 0.1π rad
Angle OSU = π(sum of angles in triangle) - (0.1πx2)
= π - 0.2π = 0.8π rad
So tedious...
Yalor very tedious hor?
If one looks hard enough at the diagram, since US = OS = VS, a circle with center S will magically materialize:
And using one of the Angle Properties of Circles (which surfaced in the little link Miss Loi included in the main article) where:
So we get ∠USV = 2 × ∠UOV = 0.4π rad
∴ ∠OSU = π - (∠USV)/2 (since it's given OR bisects ∠POQ) = 0.8π rad 😉
曜
日
Yes to find the shaded area, your approach is summarized as follow:
Area of Sector OPQ (= 3.6π cm2 obtained in 1ii. above)
- Area of Sector USV
- Area of Δ OSU
- Area of Δ OSV
2. By symmetry, angle OSV = angle OSU = 0.8π rad
Angle USV = 2π(angles at a point) - (2 x 0.8π)
= 2π - 1.6π = 0.4π rad (which is obtained directly if one has used the 2nd method of calculating ∠OSU above - but follow whichever method you're comfortable with)
Area of sector USV = ½ (SU2)(0.4π)
= ½X9X0.4π =1.8π cm2
Again by symmetry, area of triangle OSU
= area of triangle OSV
= ½(OSxSU)xsin0.8π
(using the ½ABsinθ area of Δ formula you've learned in your Sine Rule chapter)
= ½x9xsin0.8π = 2.645cm2
(4 sig fig, from calculator)
So shaded area PRQVU = sectorOPQ - sectorUSV
- trianglesOSU&OSV
= 3.6π - 1.8π - (2.645x2)
= 1.8π - 5.29 = 0.365cm2 (YEAH!)
(using calculator π, rounding off ans to 3 sig fig)
It's long past 2pm... The cutie π girl is very touched by you burning the midnight oil for her! <3<3<3
曜
日
Thanks to WS, may our cutie π girl finally find her true love on March 14 1.59pm 2009.
*Wonders where would WS be on that day* 😛