
circa Early Jurassic Period
Despite sounding ominously like … umm … a local translation of the word diarrhoea, loci (singular: locus) take us back to prehistorical times where intellectual cavemen students couldn’t afford the luxury of our sophisticated counting machines.
Instead, archaeological digs on fossilized remains have uncovered conclusive evidence that they rely on rudimentary tools like the Oxford Math Instrument Set to solve their E-Maths problems, provided they remembered to bring them to cave class, tightened their compass screws, and had their pencil lead refilled.
More importantly, well-preserved expressions of glee on their fossilized faces confirmed that locus is really a fun, cutish topic that’s easy to score. Have a look at this typical question discovered scrawled in a cave carbon-dated to a million years ago:
Vertices A and B of a triangle are 14 cm apart, vertex C is 11 cm from A and 8 cm from B.
- Using ruler and compasses only, construct the ΔABC.
- On the same diagram,
- construct, for all points inside the triangle
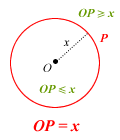
- the locus of point P such that AP = 10 cm.
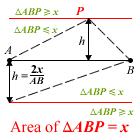
- the locus of point Q such that area of triangle AQB < 21 cm2.
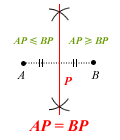
- the locus of point R such that AR = BR.
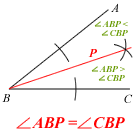
- construct the locus of point S such that ∠ ASB = ∠ ACB.
- construct, for all points inside the triangle
- Y is a point in the triangle such that AY ≤ 10 cm, the area of ΔAYB < 21 cm2 and BY ≤ AY.
Indicate, by shading, the region in which Y must lie.
This time round, Miss Loi is going to be nice and contribute to Science by revealing some of the hieroglyphic drawings discovered alongside the question in the cave:
She also urges all budding archaeologists to study the next two drawings from the neighbouring cave of the Angle Properties of Circles well, as they often tend to go hand-in-hand:
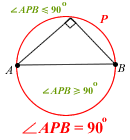
Note: Red = locus P and Green = inequality region
As you can see, locus questions haven’t really changed since neanderthal times. Basically you’ll be asked to partition and chip away your drawing one-by-one till you discover utopia in the form of some puny shaded area.
Which means you’ll need to pay particular attention to the green parts of Miss Loi’s diagrams.
Here’s some more loci notes for the benefit of mankind:
- You’ve been asked to CONSTRUCT i.e. you must use your antiquated mathematical instrument, even though you’re not a retro person. Don’t agar-agar anyhow use ruler to draw.
- Even though it might seem like a lot of work, each part typically carry only 1-2 marks, so you’ll have to be FAST and master your compass/protractor wielding skills.
- Those little crosses and arcs carry working marks! Miss Loi once had an aspiring fine-arts student who actually painstakingly erased every little arc and pair of crosses on her finished loci diagram, so that it looked nicer! Oh dear.
With so many givens, this should be the easiest Jφss Sticks question ever.
So easy in fact, the cavemen must be ROTFLMAO-ing in their fossilized graves right now.
P.S. If you’ve drawn your solution and want Miss Loi to check for you, scan it and email as an attachment to missloi [at] exampaper [dot] com [dot] sg.
P.P.S. This should also be the most cheong hei question post ever. Remember the cruel irony of short questions?.

 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 





















30 Comments
曜
日
question.. for the locus of point Q such that area of triangle AQB
曜
日
gahh nvm
曜
日
Oh no,spam.
Haha I think i know how to do 😀
曜
日
Kiroii, most likely there's some invalid character in your comment that's preventing it from displaying fully.
Could you please kindly email Miss Loi the full text of what you wish to type in the comments and we'll put it in for you ok? 🙂
曜
日
Winston, kiroii is not a spammer. On the contrary, he's been a faithful solver of Miss Loi's questions!
曜
日
*apologises hmm actually i got the answer but jus for curiousity for the area it gave the area 21 but should i use 21 or 20 to calculate the height?
曜
日
hey wad de i can comment now? w00t hmm actually the answer doesnt require that precision of 20 or 21 area.. but since its loci if used wrongly de examer may deduct marks so jus tryin to get a comfirmation
曜
日
Kiroii, note that the question states that the area of triangle AYB < 21 cm2.
So the limit is at 21 and 20 (or 20.999 for that matter) will never come into the picture i.e. don't worry about 'precision' here.
Remember that the locus in this question should be represented by a dashed line (vs a solid line if area of triangle AYB ≤ 21 cm2).
So have you drawn up your diagram yet? 🙂
曜
日
er yea but i dun have a scanner plus i dun see de point drawing on paint-__- so yea but im rather sure my ans is correct-___- since i followed all de steps =x
曜
日
but if u were to use 21 u'll get the height as 3 but if u use 20 the height will be a decimal? and i was under the impression that the examiner would check the length of the loci n stuff to check the accuracy?
曜
日
Kiroii, the question says find the locus of point Q such that area of triangle AQB < 21 cm2.
This means the upper limit of this area is 21 cm2, which is defined/bounded by the locus Q with the height of 3 cm, as you've correctly calculated.
Forget about 20 here, it's irrelevant.
曜
日
huh? but it says
曜
日
..dots here the comment flush comes again..uh but the parameters say greater then 21 but if you use 21 and get height as 3 and when you recalculate the area, you'll get the area which is 21 and therefore against the parameters? hmm btw when everyone's done with de question ya mind revealin the ans to check please? =x
曜
日
Let's do a little tuition here shall we?
It's important to note that a locus represents the movement of a point according to a rule, which means that it could be a straight line, a curve, or a region with a boundary.
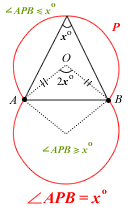
Take a look at this diagram:
As explained, the straight line locus P represents all points where area of ΔAPB = 21.
But that's not what the question is asking. It asks for the locus where area is less than 21.
When you see an inequality here (i.e. the < sign), typically you're looking for a locus that is a bounded region, which is indicated by the shaded area in the above diagram.
So to answer Kiroii's question, as long as the point Q lies within this shaded area, the area of ΔAQB will be less than 21 (could be 20, 19, 18.5, whatever ... ). But to define this area we need to know its boundary, hence h = 3.
NOTE: Notice the straight line is now represented by dashes instead of a solid line? Why? 🙂
曜
日
Good answering, Ms Loi.
曜
日
uh its represented by dashes due to the fact that its a loci? or maybe due to miss loi's fetish fer red lines? =x?
曜
日
btw mis loi is there a place where i may post a maths queries?
曜
日
I suppose it could be because as the point moves through the region covered by the loci, the lines of the triangle moves accordingly and therefore, it would move with the point going thru the loci,hence only dotted lines are used to notate the current position of the lines.
The area of a triangle is (pri sch ah) 0.5(base)(height), so if a height of 3 cm gives you an area of 21, to decrease the area such that it is less than 21, we can decrease the height---> realize that at any portion of the area below h=3, using the Formula to find area of triangle,you get something less than 21.
The base is a constant, the half is a constant, while the only variable is the height. Hence decrease the height to decrease the area. You can't change the base as it is a constant...
曜
日
huh? i know the point of using the dotted lines but i dun see why its red maybe to accentuate or differentiate them i guess..
so ur saying with the height as 3 the area within the loci is below 21? u sure?
曜
日
Actually the point is dotted lines- just the dotted lines that you needa understand.
With the height at 3, the area is instead ALWAYS 21, as the height- being the same- does not change, and hence the area does not change.
The area changes with the height.
曜
日
i know de area changes with the height -.- duh! but the dotted lines are supposed to be the loci? but since its red im wondering its probably to "strike" out or something
曜
日
The dotted lines are the loci, and that locus is the boundary.
A important point i missed out is that the line is dotted because as a boundary 3cm away, we know that if height
曜
日
Oh no there is something wrong with the posting-- it ate away more than half.
Dotted line used as the boundary cannot touch the line or area would be 21 already.Hence cannot touch the line,and dotted lines used.
If you want area to be less than or equal to 21, then u use a solid line as the line is included as a permitted part for the point to get that area..
曜
日
er ok..tats indepth anyway thanks got it through my head
曜
日
No problem,my pleasure.
Solid: Included in the locus.
Dotted line: DO NOT count it in!!!
曜
日
Wah that's a lively exchange in Miss Loi's absence.
To settle it once and for all,
1. Yes, as Kiroii pointed out, the red is to accentuate/differentiate the loci P and Q (to tie in with the corresponding colors in the notes below).
And no, Miss Loi doesn't have fetishes of any sort (at least nothing that she'll admit here).
2. For a region with a boundary, as winston pointed out, a solid boundary line means that this boundary is included in the region, and vice versa for dashed line.
Notice the difference in the green inequality statements adjacent to the boundaries in the various diagrams?
P.S. The comment cut-off problem has been solved (somewhat). Basically it's the problem with the < character - the comment will be cut-off beyond this.
For now please use < to replace your < in your comments. It will automatically translate to the 'less than' symbol.
曜
日
wait wait miss loi!! u 4got to ans my question is there a place to post maths enquries?-_- there are certain questions which even my teacher cant do so -.-""
曜
日
Oops sorry missed that.
Please email me your maths enquiry one at a time and I'll try my best to answer asap.
Of course, do be gentle with my inbox ... 🙂
曜
日
eh ya mean missloi [at] exampaper [dot] com [dot] sg ?
Edited the email coz Miss thinks this is the reason she got two mails from Nigeria this morning 🙁
曜
日
kindly help me by solving this problem
the locus of point R such that AR = BR.
this is part c of q2