In a serious case of deja vu, the evil cats and dogs came pouring from the heavens with a vengeance late Thursday afternoon.
This time though the newly-reinforced roof of The Temple managed to hold its own, leaving an immensely relieved Miss Loi to continue marking her students’ homework.
As if to prove that a special telepathy bond exists between the owner and her pet, Miss Loi sensed a disturbance in the apparent serenity when she could almost hear a faint mechanical “help!” coming from the direction of … THE CARPARK!!!
Like a desperate heroine to the rescue of her lover in distress, Miss Loi bolted passed the Temple Gates to stand before the scene of carnage that greeted her.
As she dashed across the road towards the carpark, with the incessant rain mercilessly ruining her makeup, she found her usual path transformed into a raging river!
Oh but a raging river is no obstacle to her determination to reach her love, even though she lacked the prerequisite dragonfly skipping water aka 蜻蜓点水 ability. And so in an emotional scene, Miss Loi threw caution to the wind and sacrificed her Charles & Keith shoes to wade through these waters to the carpark.
After what seemed like an eternal trudge through the waters, she finally spotted her fragile object of love – cold and weakened, and stranded on a patch of dry land surrounded by menacing flood waters. Tears filled her eyes as she threw aside her umbrella (no she didn’t) and rushed forward (in typical slow-motion) to an emotional reunion under the pouring rain.
Sorry too overwhelmed at this moment for photos
Upon recovering from that dramatic moment, Miss Loi found to her dismay that the exit route was awashed with more evil floodwaters!
A quick call to her exclusive oracle in the Meteorological Station revealed that the rain will stop in exactly 50 mins time. But ominously, the large longkang ala monsoon drain beside her car is filling up fast!
A decision has to be made now as to whether to Miss Loi should drive through the floodwaters and make a run for the exit, or wait out the next 50 mins and risk getting her Charles & Keith shoes ruined further if the drain overflows.
Once again, using her amazing mathematical analysis powers …
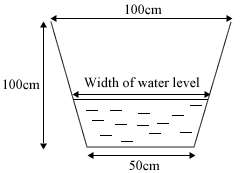
The cross sectional profile of the drain is uniformly trapezoidal with two equally sloping sides, a depth of 100 cm, a base width of 50 cm and a maximum width of 100 cm at the top.
Given that Miss Loi has just witnessed the width of the water level rise lengthened alarmingly in a constant manner from an initial 60 cm (at the time she called the Meteorological Station) to 70 cm in just 10 minutes. determine if the height of the water in the drain will overflow within 50 mins.
*Find the rate at which the height of the water in the drain is rising, and hence determine if the height of the water in the drain will overflow within 50 mins.
*re-phrased thanks to someone ‘hacking‘ this question!
Can you please help Miss Loi decide? As far as possible she wants to avoid ending up like this!
NOTE: Unfortunately, this is based on a true story.
17 Comments
曜
日
Oh my! I need to put some of your car flooding stories on my blog soon!
Anyways, the same time you were going through this, I was driving back from KL to Singapore. A usual 3-4 hours drive took me more than 6 hours due to the extreme weather where visibility was less than 10 metres and a couple of rather major accidents were witnessed on the north-south which not only slowed traffic but slowed my accelerator pedal too!
曜
日
Hmm..Let's hope the water will overflow and then I can make some soup!
After some calculations: Area of the increase in height =
*The above calculations can be used if you forget the area of trapezium formula..Just split it into rectangles and triangles!
The amount of area filled per minute
Assuming that the 10 minutes Miss Loi used is wasted, there is 40minutes left and the area filled in this time is then
Area of trapezium left =
Since the area filled is more than the area left, there would be
length of road of soup for everyone to drink!
*Assuming that all my calculations in the head work out correctly. Soup is old and tend to make careless mistakes!
曜
日
Oh my! I empathise with your situation, especially with the loss of the Charles & Keith shoes. Is your mechanical pet okay?
曜
日
It's time to seek higher grounds!
曜
日
Time to Scuba? :p
曜
日
Think it's time for smc to pray to the Almighty Sun God to shine ferociously down and chase away all the rainclouds at Novena 😀
曜
日
HighwayBlogger: Usual 3-4 hour for KL-Sin? Did you rest along the way? If you did you're fast! If you didn't you're a safe and patient driver along the NS Highway 😀
Precious: Safe to say that both owner and pet survived the ordeal in the end. But sadly, the same can't be said of Charles & Keith, given their quality these days 🙁
Peewee: Miss Loi (and most importantly the car) was already at the highest ground!
Arzhou: Vis too poor. See what? See longkang fish?
FoxTwo: Over here in Novena, the Sun God appears to work only half-day shifts. Super duper hot in the morning and then ...
曜
日
Wah Soup ... Miss Loi only mentioned that the width of the water level (let's call this x) is lengthening (ok let's be more specific here)/changing at a constant rate i.e.
is constant.
But by simply dividing the change in area (A) (which is in another dimension) by 10 mins you are implying that
is also constant.
Are you absolutely sure?
曜
日
Hmm, I have two methods for this method, I'll just show the simpler one, though frankly, i'm also not too sure 🙂
Here it goes:
Let x be the width of the water level, with 60cm as the starting and 100cm being the max level. Assume that the change of x with respect to time is constant (though it's weird...cos it means that the rain must be getting progressively heavier and heavier, not exactly what I can imagine when the meteorological station says that the rain will stop in 50 mins time...oh well)
60 to 70 cm takes 10 min
70 to 80 cm takes 10 min
80 to 90 cm takes 10 min
90 to 100 cm takes 10 min
In total, it'll take 40 mins for x to reach 100 cm. Another longer than that, the water will over flow out.
My spidey sense is tingling...so Miss Loi pls point out any wrong assumptions I've made, thks!
曜
日
Haha Papillion,
My bad my bad ... in her neverending quest for the dramatic, Miss Loi was too complacent to see this obvious shortcut coming from the blindside 🙂
Guess you already know that this is a question on Rate of Change, so she should better rephrase to the following:
Oh and with the weather these days, please don't even predict how the rain will behave!
Bring on your Chains!
曜
日
hmm i assumed that the amount of water that drops inside is constant..and hence, the amount of area occupied per unit time should be the same? lol..niwae just did that for fun whilst doing my C++..
曜
日
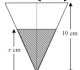
Considering the full triangle, with x as the 'chopped off' length, by similar triangles,
w is the width at any particular time, by similar triangles,
In 50 minutes, the water will have risen by another
,
25cm100cm; from an initialTo give a final height of
40+25=65 cm; which is less than 10040+2(50)=140>100,
overflows
Once again Miss Loi has inserted a diagram for readers to better understand your solution - especially on the whereabouts of your 'chopped-off length' x 😛 For your solution Miss Loi was just about to pounce on you until she saw your next comment!
The Chain Rule and similar triangles are definitely required to solve this Rate of Change question (Papillion's epic shortcut nowithstanding) 😛 😛 😛
Miss Loi's similar triangles are a little different - though the final answer is the same, but once again it's great to be able to highlight that there's often more than one way to solve the same question 😀
Miss Loi's solution coming right up ...
P.S. Thought the initial water level width was 60cm (not 70cm)? Hence initial h = 2(60)-100 = 20. CARELESS MISTAKE! Tsk tsk.
曜
日
Please pardon me if I have any errors, I'm kind of tired now. Haha.
曜
日
Rate of Change questions are pretty straightforward and will almost always involve the Chain Rule i.e. given an expression y = f(x),
Most Rate of Change questions in your Ten-Year Series are quite kind to state explicitly the variables involved and their relationship i.e. y = f(x)
But others, like this one, requires you to read the question carefully to determine the variables and their relationship.
1) So from the question, you're supposed to find the rate of change of the height (h) of the water level i.e.
2) But you're given that the width of the water level (w) is lengthening constantly, which means you can obtain
by simply
3) But from the Chain Rule
we'll still need to form the expression for the relationship between h and w in order to obtain 
.
So ...
See the two little right-angled triangles formed at the sides?
Taking one of this triangles to form the following similarity ratio, can you see that:
So at any given time, the water level w can be expressed by:
and viola we have you relationship between h and w!
So
which is exactly the same answer as Someone's!
Which means that the height of the water is rising at 2 cm per minute, and in 50 mins it would have risen by 50 x 2 = 100 cm.
And since it's given that the initial width is 60cm, from (1)
⇒ initial height = (60-50) x 2 = 20 cm
⇒ height = (20 + 100) cm = 120 cm in 50 mins!
⇒ OVERFLOW!
⇒ It was REALLY scary driving the car through the flood! Miss Loi felt like she was driving a boat!
曜
日
I was under the impression it was 70cm after 10 minutes from -10 min as the start, with 50 minutes counting down from the 70cm mark. Haha...
曜
日
Could you help insert my correction into my original post? It will make more sense to readers. Haha.
曜
日
Someone: Done. Your wish is Miss Loi's command 🙂
Regarding the starting time in the question, Miss Loi actually meant it to be from the point the phone call is made (hence the word initial in the question). But having reread the question, she found that this can be open to different interpretation so she should just state this clearly the next time :P.
In any case, it'll still overflow regardless!