For 2007 O-Level students in Singapore, Tuesday was an important day when the Joint Admissions Exercise (JAE) results were released, when their places in the institutions (hopefully of their choice) were confirmed, when they can finally leave their O-Level lives behind and focus on that chick/hunk they have been eyeing throughout the PAE period.

For a particular Student, it has always been his life-long dream to study in Elite Junior College (EJC), nestled high in the mountains above the clouds where elite eagles soar, where students there were taught the legendary Four As Guaranteed Explosive Mugging Technique that would ensure their A-Level success.
He was quietly confident that, with his raw L1R5 score of 7, he would claim his place among the elites at EJC. After all his dad was an elite EJC alumni who got in with an L1R5 score of 9 decades ago.
So it came as a total shock to him on Tuesday when he was posted to Non-Elite Junior College (NEJC), nestled in a kampung by a muddy river bank where chickens roam.
Undeterred by this setback, The Student, together with his dad, made a great journey across the plains by MRT, and climbed a thousand steps up the mountain to the gates of EJC, where they sought to appeal his posting before the sagely principal of EJC.

Predictably, the principal turned them away, informing them that all places in EJC had already been filled by guinea pigs IP students as well as those who got their L1R5 minus-ed here minus-ed there through being former students of Elite Secondary School (ESS) and a host of other things.
But such was The Student’s determination to meet the hot girls of EJC master the Four As Guaranteed Explosive Mugging Technique that he vowed not to leave till he was accepted, despite his dad’s protestation that they were going to miss the last MRT train home.
And so for days and nights they knelt outside the gates of EJC, father and son, battled by the howling rain and ogling at passing EJC girls for temporary respite, imploring the principal to accept The Student.
By the end of the third day, the principal was sufficiently disturbed from his sleep by their constant KPKB moved by The Student that he threw him this math question, promising his acceptance into EJC if he could answer it:
The angles A and B are such that
A + B = 120o
cosA + cosB = 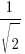
Show that 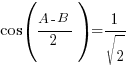
Hence find the possible values of A and B, given that 0o < A < 120o and 0o < B < 120o.
The principal chose this question as it happens to be on the list of assumed knowledge for the H2 Mathematics Syllabus. It also hails from the New O-Level A-Maths Syllabus, where the Factor Formulae are now included in the Trigonometry component.
So to enter EJC, apart from knowing the trigonometric values of special angles (hope he brought his textbook along!), and remembering that All Science Teachers are Crazy Diagram, The Student also has to utilize one of these Factor Formulae (especially when something like cos A ± cos B occurs in the question):
sin A + sin B ≡ 2 sin( ) cos(
) cos( )
)
sin A – sin B ≡ 2 cos(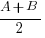 ) sin(
) sin(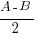 )
)
cos A + cos B ≡ 2 cos(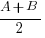 ) cos(
) cos(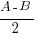 )
)
cos A – cos B ≡ -2 sin(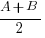 ) sin(
) sin(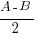 )
)
But surprise, surprise. Since he belongs to the 2007 batch of students who took the OLD A-Maths Syllabus, like many JC1 students right now, this is totally alien to him – which is why he needs YOU current O-Level students to help him get into EJC!
Meanwhile,
Good luck to those of you awaiting your appeal outcome this week!
P.S. Do note that the above story does not accurately reflect the actual JC appeal process in Singapore.


 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 





















18 Comments
曜
日
Lol this question is easy. Just use factor formulae and the fact that cos60 is 1/2.
曜
日
Soup, NWNT.
曜
日
Haha..






曜
日
OMG Soup! You should be proud that you're the first commentator ever to have successfully used the math plugin to answer a question here!
But umm .... you do know that you can use {braces} as 'invisible brackets' to make your workings 'neater'? i.e. reduce the number of visible brackets which Miss Loi has changed for you.
Looking at the ease of your solution, Miss Loi sort of regretted 'spoon-feeding' the Factor Formulae as one of the keys to the solution. In fact in Miss Loi's tuition sessions it has always been: no hints = student will complain question was difficult, give a small hint = student will say question was soooo easy.
Unfortunately students have to realize that in the actual exam, you won't find a similar question that says "Use the Factor Formulae to show that ..." 😛
In any case one must always remember, that as a Trigo A-Maths pugilist, he/she needs to know when to draw the right weapon from the whole arsenal of trigo formulae at his/her disposal (be it Factor Formula, R-Formula, Double-Angle Formula, Addition Formula, Sine/Cosine Rule blah blah blah) - regardless of whether they are shown in the formula sheet.
Such is the essence of mastering the Four As Guaranteed Explosive Mugging Technique ...
After so much talking, Miss Loi just remembered that there's still a Part 2 to this question!
曜
日
I'm just glad I am not making a machinima out of this story 😀
曜
日
Lol.. I'm the first? Hahaha.. I think the pmath plugin is great. A pity that it can't work on my own site though. Some PHP library ain't installed..
曜
日
Fox, the Four As Guaranteed Explosive Mugging Technique too hot for your machine to handle? 😉
Soup, that's a pity. Miss Loi found it much more intuitive to type out equations using this as compared to the old LaTeX plugin whose cryptic syntax she never quite managed to figure out. 🙁
曜
日
Um, no. No maths plugin for machinima :p
曜
日
Wahaha, the 2nd picture was really LOL-zable :D!! Nice one man :P! Cheers!
曜
日
Wah lau...2nd pic taken from kill bill?
曜
日
ASM, please be serious and don't anyhow laugh at the sagely Principal of EJC, lest he plucks out your eye!
OMG Pai Mei?! Thought you're already dead?! *scampers away to save her eyeball*
曜
日
Sorry, me dunno how to use the syntax. Anyway, here's the part 2:
Since = cos (45°),
= cos (45°),
 = 45°, 315°
= 45°, 315°
Thus
Yes, whenever you see phrases like "find the values of x ... given that A° < x < B°" blah blah blah ... you'll know you're dealing with the All Science Teachers are Crazy diagram and there'll be some work on your hands!
You've already proved in Part 1 that and so the basic angle of
and so the basic angle of  , α = cos-1
, α = cos-1 = 45°
= 45°
And since 1/(√2) is positive, it follows from the SATC diagram (A and C quadrants) above that = 45° or (360-45)° = 315°
= 45° or (360-45)° = 315°
IMPORTANT: We only did one 'round' of the 360° circuit since the 'coefficient' of (A-B) is ≤ 1. More 'rounds' are usually required when the 'coefficient' > 1 - refer to your textbook if you're lost or see this example for a rough idea.
2012 Update: NOT SO FAST!
Thanks to Ryan for pointing out, there's a tricky part to this question which apparent everyone has missed in 2008!!!
It's vital to consider the range of when deciding its possible values.
when deciding its possible values.
In this case the max value of = 60° (Amax − Bmin/2) and its min value is −60° (Amin − Bmax/2), so
= 60° (Amax − Bmin/2) and its min value is −60° (Amin − Bmax/2), so
−60° ≤ ≤ 60°
≤ 60°
Many of us are so used to the anti-clockwise circuit as the majority of such trigo questions has 0° ≤ x ≤ 360°, but in this case the range goes into a negative region. So while 315° lies outside the range of , its 'corresponding' angle of −45° in the same quadrant does lie inside its valid range, since cos(−θ) = cos θ. Thus it's imperative you consider going around the clockwise (negative direction) when you see a range in the negative region!
, its 'corresponding' angle of −45° in the same quadrant does lie inside its valid range, since cos(−θ) = cos θ. Thus it's imperative you consider going around the clockwise (negative direction) when you see a range in the negative region!
So ...
(A-B) = 90°, 630°A = 90°+B, 630°+B --- (ii)(A-B) = 90°, −90°
A = 90°+B, −90°+B --- (ii)
Since A+B = 120° --- (i),
Sub (i) into (ii)
(90+B) + B = 120°, (630+B) + B = 120°90 + 2B = 120°, 630 + 2B = 120°B = 15, -255 --- (iii)(90°+B) + B = 120°, (−90°+B) + B = 120°
90° + 2B = 120°, −90° + 2B = 120°
B = 15, 105 --- (iii)
Sub (iii) into (ii)
A = 105°, 375°Since A & B lies between 0° - 120°,
Thus the values are:
A = 105° & B = 15°.A = 105° & B = 15° or A = 15° & B = 105°.
曜
日
@Soon: Your answer is only partially correct. (A-B)/2 = 45 OR -45.
[*not* 45 OR 315, since (A-B)/2 ranges between -60 and 60]
Hence, the complete solution set is [A=15, B=105] OR [A=105,B=15].
Plug both solutions into the given info and see for youself that they both work!
曜
日
@Ryan: Thanks for pointing this out!
Many of us are so used to the anti-clockwise circuit through the quadrants as the majority of such trigo questions deal with the range of 0° ≤ x ≤ 360°.
But in this case, a clockwise route needs to be considered as well since the range has a negative region. Miss Loi has updated the explanation in the original comment.
It's amazing how everyone (including yours truly) missed this out in 2008! So it's not so straightforward to get into EJC afterall eh?
曜
日
*Sneaks in quietly to tidy up Soon's solution and add some explanation ... *
曜
日
If that problem was the only requirement to enter an EJC I would be happy since I'm in secondary 1 but I can solve that problem (with some reference to the sum-to-product formulae as I can't seem to memorise them yet).
曜
日
Unfortunately, with the ever-evolving IP stuff these days, the real principals may not be as magnanimous and forgiving as our benevolent Principal of EJC.
Do continue to work hard in your quest towards your mastery of the Four As Guaranteed Explosive Mugging Technique one day.
曜
日
I realised I didn't attempt this question.
One thing I don't understand, if the original question already stated that cos A + cos B = 1/root 2 AND A + B = 120, by commutative law doesn't it already imply that if (A,B) = (15,105) then (B,A) can also be (15,105)? i.e. (A,B) can also be (105,15)?
That saves the trouble of going to the negative region of the C quadrant.