… continued from here.
Night has fallen again.
After two nights of playing catching with the Chinese Vampire, Miss Loi finally obtained the Divine Coefficient and stopped the maths-tuition-deprived 僵屍 in its track.
But there was no time to lose. Making sure she remembered to take the precious Gucci bag that she bought with a big discount in the last GSS, she quietly tip-toed past the paralyzed vampire.
As the movie script fate had it, a gust of wind swept into The Temple when she opened the door, blowing that yellow Post-It off the vampire’s head.
As the 僵屍 began hopping again, Miss Loi now had to flee (as fast as her pair of cheap Charles & Keith shoes would let her) down the 38 Steps towards her own salvation – passing the Three Signs to The Temple along the way – an irony considering that hundreds have climbed in the opposite direction towards their salvation.
As the 僵屍 began hopping again, Miss Loi now had to flee (as fast as her pair of cheap Charles & Keith shoes would let her) down the 38 Steps towards her own salvation – passing the Three Signs to The Temple along the way – an irony considering that hundreds have climbed in the opposite direction towards their salvation.
As the 僵屍 began hopping again, Miss Loi now had to flee (as fast as her pair of cheap Charles & Keith shoes would let her) down the 38 Steps towards her own salvation – passing the Three Signs to The Temple along the way – an irony considering that hundreds have climbed in the opposite direction towards their salvation.
After developing stomach cramps from all that running, Miss Loi whipped out her ancient Nokia N73 again to call the moonlighting temple medium friend:
HEY WHAT’S GOING ON?! Why am I seeing the same scenes over and over again like I’m being COPY-AND-PASTED?! I don’t remember the stairs being so long!
After a brief moment, came this reply:
天灵灵地灵灵 …
Oh my Sexy Maths Tutor, you are now trapped in the realm of the Undead, somewhere in the region bounded by the following inequalities:
- x2 – 11x + 18 > 0
- x2 – 11x < 0
To return to the Realm of the Living, you have to use the above inequalities to find the region bounded by range of x that satisfies the inequality
|x2 – 11x + 9| < 9
As the 僵屍 began hopping again … Miss Loi would like to remind all students that for a typical quadratic function f(x) with two real distinct roots (α and β) and a positive coefficient of x2 (it’s always a good practice to make this positive as a first step), the ranges of x for its regions of quadratic inequalities can be summarized as follows:
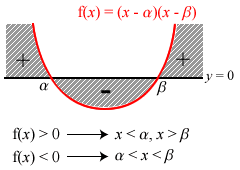
Please pay particular attention for the case of f(x) > 0 – students tend to get caught by 僵屍s here!








 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 





















4 Comments
曜
日
Miss Loi is now marking your solution while running down those infinite steps ...
Instead of risking life and limb and try to solve that scary-looking modulus function directly, it's always a good idea to follow what the question tells you i.e. use the given inequalities to find your final answer (as you've done below). Note that this is another example of a Hence question.
Solve inequality 1 and 2:
x2 - 11x + 18 > 0 and x2 - 11x < 0
(x-9)(x-2)>0 and x(x-11)<0
(x<2 or x>9) and 0<x<11
.'. 0<x<2 or 9<x<11
Factorising x2 - 11x + 18 quickly via the Trial & Error method (or otherwise), you'll get (x-9)(x-2) > 0.
Ensuring first that the coefficient of x2 is positive (hence a U-shaped curve), it's clear from the following diagram that x< 2 or x > 9, since we're finding the range of x for the region(s) > 0.
NOTE: Whenever you're dealing with > 0 (for a U-shaped curve), please DON'T make this common mistake of e.g.
(x-9)(x-2) > 0 ⇒ x > 2, x > 9 ⇒ WRONG!
The second case of x(x-11) is more straightforward as we're interested in the single region that is < 0 in diagram below:
Next we shall first extend a warm welcome to Modulus Functions to this year's A-Maths O-Level Syllabus 😉 For this question, it's important to note that for an arbitrary constant k ≥ 0:
|x| < k ⇔ -k < x < k
|f(x)| < k ⇔ -k < f(x) < k
|x| > k ⇔ x < -k or x > k
|f(x)| > k ⇔ f(x) < -k or f(x) > k
*Doesn't this follow the same pattern as our quadratic inequalities diagram above? 🙂
** Can k ever be < 0 for any modulus expression?
From |x2 - 11x + 9| < 9 we get
-9 < x2 - 11x + 9 < 9
And so we now know that |x2 - 11x + 9| < 9 can be spit into:
x2 - 11x + 9 > -9 ⇒ x2 - 11x + 18 > 0
x2 - 11x + 9 < 9 ⇒ x2 - 11x < 0
Which are the two original inequality expressions in our question! Which also means that the solution to |x2 - 11x + 9| < 9 is obtained from the range of x that satisfies both the two original inequalities.
i.e. x2 - 11x < 0 and x2 - 11x + 18 > 0
Solving this compound inequality gets the same answers above.
.'. The required range is 0<x<2 or 9<x<11.
Yes this can be seen clearly by representing the solution sets of the two inequalities on a number line:
You'll see that the ranges that satisfies both the equalities are 0 < x < 2 and 9 < x < 11 (i.e. the red regions that overlap both solution sets.
*N.B: Note that that the little cute circles are white ○ in the number line coz it's < / > (exclusive). You should use cute little black circles ☻ instead in situations when there's ≤ / ≥ (inclusive) in your inequality expression.
曜
日
i hate Maths.
曜
日
Solving inequalities with absolute values was once in the HKCEE A. Math syllabus but its final appearance was the 2003 paper. Since then it was cut from the syllabus. Solving this took some time; I needed to think it over. (I didn't know it was also called modulus function.)
Can you escape from the recurrence now?
曜
日
Wah Cendrine such a big reaction - 发生什么事?!
Li-sa: Modulus functions are out of HKCEE but in for Singapore's A-Maths 2009. Thanks to you, Miss Loi is now making a phone call at district 0 < x < 2 or 9 < x < 11 and hopes to have escaped her version of Groundhog Day 🙂