It was noon at The Temple when Miss Loi was totally engrossed in trying to obtain the proof in a nasty Plane Geometry question sent earlier by a student.
After staring for what seemed like an eternity at the question’s diagram, her 阴阳眼 simply would not come and she was beginning to get very tired, partly due to the ridiculous phone call that cut short her sleep in the morning.
Never one to give up easily in the face of adversity and face the ignominy of hearing a “Haha! Miss Loi also dunno how to do!“, she rubbed her eyes and continued to stare intensely at the diagram.
So intense was her gaze that a circle in the diagram seemed to grow larger and larger as it beckoned her to lean closer and closer … so close that she felt almost at one with the question and could almost feel the closeness of the solution that she desperately sought.
Suddenly, an unknown force reached out and, to her horror, pulled her headfirst into the circle!
In the harrowing moments that followed, she was whisked through a tunnel lined with circles, triangles, tangents, secants, chords and all manner of grotesque polygons from the O-Level A-Maths Syllabus.
After what seemed like an eternity, she landed with a big thump right in front of a weathered-looking Right-Angled Triangle (RAT), who muttered
Oh boy here comes another 走火入魔 one.
Who are you? Where am I?
asked Miss Loi as she meticulously checked for any facial scar arising from the rough landing.
You’re at the Plane of Geometry. The realm of all killer Plane Geometry questions. And you, of all people, should know that I’m the Right-Angled Triangle alias Pythagoras Theorem – introduced to most during Sec One/Two and some say even PSLE! But they hardly think about me anymore.
Can you show me the way back to The Temple?
The RAT continued to grumble.
These days all the young people here only care about the ‘latest’ fads like the Tangent-Secant Theorem etc. They hardly think about me anymore.
Uncle! I really need your help! I’ve got a class to teach in a few hours’ time! AND I WANT MY NATIONAL DAY LONG WEEKEND!!!
I will show you the way if you can show me the following:
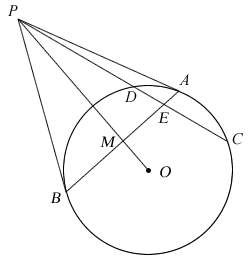
P is a point outside the circle such that PA and PB are tangents to the circle of centre O. M is the mid-point of AB and the secant line PDC cuts the chord AB at E.
Show that:
- ΔPMA is similar to ΔBMO
- PA×BM = BO×PM
- PE² = PD×PC − DE×CE
As Miss Loi has somehow lost her 阴阳眼 ability, can you help her find her way back to The Temple?
Meanwhile the RAT continued to mumble …
They hardly think about me anymore …
8 Comments
曜
日
Miss Loi: Nothing like a diagram to brighten up your workings and a National Day 😉
let these 2 angles be y.Therefore, Angle BMP= Angle AMP= 180-y
Think you'd agree this part is unnecessary for the final working.
let angle ABO= x, hence Angle BAO= x
(BO=AO cos they are both radii, hence triangle ABO is isosceles and base angles are equal.) Angle BOA= 180-2x
(Ok Miss Loi, this is the part where I am not sure. Please point out if there's flawed reasoning... D:)
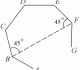
Alright may this little diagram on the right (taken from the official Jφss Sticks Plane Geometry cheatsheet) help firm up your reasoning to a steely level.
Given that M is the mid-point of AB, and recalling the Perpendicular Bisector of a Chord property which most of you would've learnt in your Geometric Properties of Circles, the line joining the circle center O to M will imply that ∠BMO = 90°.
And by taking the interior angles of ΔBMO we can obtain ∠BOM straightaway as 180° − 90° − x = 90° − x = ∠PAM.
P.S. This in turn will also confirm chop stamp prove that PO bisects ∠BAO, since PAOB is actually a layang-layang kite.
Angle PAO= 90 degress (tan. perpen. rad)
And since Angle BAO= x, Angle PAM= 90-x.
PO bisects Angle BAO, hence angle BOM= (180-2x)/2
= 90-x.
Therefore Angles PAM and BOM are the same and both triangles PMA and BMO are similar (AA)
Hence, shown. Yay! One step closer to Miss Loi's liberation ...
曜
日
Wait... that was only the 1st part.
曜
日
Part 2)
And since the two triangles are similar,
cross multiplying, PM x BO= PA x BM (shown)
This part is sooooo simple that Miss Loi couldn't believe that it originally carries 2 marks! Maybe a mark for saying "since the two triangles are similar" and stating and cross-multiplying the ratio from the following:
And the final mark for the final answer. Such a giveaway that Miss Loi will *kok* the head of any who can't answer this!
曜
日
since its late, shall continue tomorrow... 😀
曜
日
As explained above, once you've found that ∠BMO and ∠PMA = 90° using the Perpendicular Bisector of Chord property, a whole new world of proving possibilities lay in wait for you.
Here's an alternative proof just for the sake of it:
Let ∠MPA = θ
∠PMA = 90° (⊥ bisector of Chord AB)
Take ΔPMA,
∠PAM = 180° − 90° − θ = 90° − θ
PA = PB (Tangents from ext. pt.)
⇒ ΔPBA is isosceles
⇒ ∠PBA = ∠PAB = 90°−θ (base ∠s of isosceles Δ)
∠PBO = 90° (Radius ⊥ Tangent)
⇒ ∠MBO = ∠PBO − ∠PBM = 90°−90°−θ = θ
⇒ ∠APM = ∠MBO
∴ ΔPMA is similar to ΔBMO (2 angles similar)
Now where's Part 3???! Miss Loi's idea of a long weekend doesn't including spending it in front of a grumpy right-angled triangle!
曜
日
Muhahaha....ms loi i solved part 3 of the qn already...(btw, no need to guess...i not ur student...juz happen to be a follower of ur website...)
- PB^2 = PDxCP
- BE x EA = DE x EC
- tri PMA is congruent to tri PMB
- Using tri PME and tri PMA,
PE^2 - ME^2 = PA^2 - MA^2
- With some simple substitution and factorisation, the qn is solved...(i think the rest is easy enough...hee hee) 🙂
曜
日
JOYL's answer stopped the Right-Angled Triangle's incessant grumbling in its track.
"Strong is this woman's mighty 阴阳眼, from the quick working-less way she obtained her prove merely "with some simple substitution and factorisation ... hee hee""
To prove the seemingly elusive PE² = PD×PC − DE×CE we first list out the relevant properties/theorems that will contain the our required line segments, as JOYL has done:
PA² = PB² = PD × PC (Tangent-Secant Theorem) -- (1)
This takes care of PD × PC in the equation.
BE × EA = DE × CE (Intersecting Chords Theorem) -- (2)
This takes care of DE × CE in the equation.
And now this is the moment when one hopes that the 阴阳眼 will come. And often it comes with the most simplest and basic of properties that you've learnt in lower secondary!
Like in this, students are so caught up trying to recall the latest theorems that they often forget about ME - the Pythagoras Theorem! Add my fellow old friends like interior angles of triangles and parallel lines to the list as well!
So ...
Since we've already proven in Part 1 that ∠PMA = 90°
ΔPEM: PE² = PM² + ME² (Pythagoras)
ΔPAM: PA² = PM² + MA² (Pythagoras)
Moving the above two equations around we get:
PA² − PE² = MA² − ME² -- (3)
This takes care of the PE² in the equation.
Now it's time for JOYL's "simple substitution and factorisation ... hee hee" part (please correct Miss Loi if this isn't your exact method ok?) ...
Now look closely at the chord AB in the diagram and using equation (2):
DE × CE
=BE × EA
= (BM+ME)(MA−ME)
= (MA+ME)(MA−ME) since BM=MA as M is mid-pt. of AB (given)
= MA²−ME²
So sub DE × CE = MA²−ME² into (3),
PA² − PE² = DE × CE²
PE² = PA² − DE × CE²
And sub PA² = PD × PC from (1):
PE² = PD × PC − DE × CE (Yay!)
So you see, one of the most crucial part of the working is being able to express PE using the Pythagoras Theorem, and recognizing that I'm not some old forgotten has-been who still is useful in Plane Geometry society! So please don't retrench me!
"Now go my Sexy Maths Tutor!" says the Right-Angled Triangle as he handed her the latest copy of the Plane Geometry Street Directory.
"You follow this straight line ... then turn left at the intersection of the two chords ... then follow this tangent ... "
曜
日
Dear Miss Loi,
Is it possible to prove that 1/PE = 1/2 (1/PD + 1/PC)?
Thank you.