On a particularly vain morning, Miss Loi was suddenly troubled by the perennial question: “Do sexy maths tutors actually exist?”
Similar feelings had surfaced in the past, and being a woman of action, she decided to settle this issue once and for all. So, to her feet she sprang and out (from an overworked photocopier) came a huge stack of leaflets containing the following multiple-choice question:
Do you think sexy maths tutors exist? Please tick ONE.
[ ] Holy Moly! You kidding me?! Yes of course!!!
[ ] No, don’t think so. Sorry, but I’m late for my optician appointment!
After some jostling with the promoters from various insurance, timeshare and credit card companies, Miss Loi managed to secure a prime spot at a busy Orchard Road junction to conduct her little survey for the good of mankind … but things didn’t go as smoothly as planned.
Many replied with a terse “Sorry already bought insurance!” when approached by her. Also, a certain k number of surveyees didn’t follow instructions and ended up ticking both boxes – it had to be said that many of these ‘culprits’ were in close attendance by their wives/girlfriends throughout the survey.
But worst of all, tragedy struck in the form of a strong gust of wind which scattered all her leaflets across Orchard Road just as she was packing up!
So …
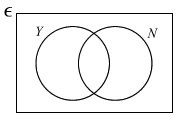
The Venn diagram was drawn to represent the sets:
ε = {all those who were approached}
Y = {those who answered Yes}
N = {those who answered No}
Miss Loi managed to recall that:
n(Y ∩ N) = k,
n(Y) = 7 x n(Y ∩ N),
n(N) = 4 x n(Y ∩ N),
n(ε) = 6 x n(Y’ ∩ N’)
- Please help Miss Loi by first inserting, within the Venn diagram above, in each of its four regions, the number of people, in terms of k, represented by that region.
Being an extremely petty personBy a stroke of luck, Miss Loi actually kept count of a total of 165 persons who spurned her approach and did not answer the survey.Calculate the total number of persons approached by her. Hence state how many of those surveyed firmly (i.e. confirm chop stamp) believe in the existence of sexy maths tutors.
This being the swansong year for Sets & Venn Diagrams in A-Maths, there’s a niggling suspicion that it’s one of those chapters that will go out with a ‘bang’ i.e. last chance for examiners to set something sinister.
To excel in the land of the Sets, most of the time you’ll have to know some of their basic local language:
 , φ, {}: Null or empty set
, φ, {}: Null or empty set- ∩: Intersect
- ∪: Union
- ⊆: Subset of
- ⊇: Superset of
- ∈: Element of
- n(P): number of elements in P
And be familiar with their diagrams:
Intersection:
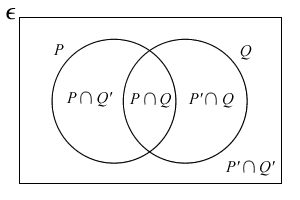
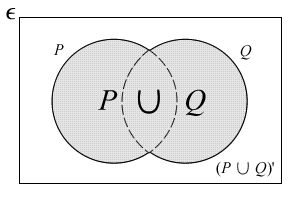
Union:
WARNING: While most students should be able to answer 75% of this question, there’s a rare O-Level twister in its remaining portion which you’ll either get it very quickly or you won’t. So if this appears in the exam, please move on to the next question if you find that you’re more or less stuck.
Your grades are more important than the existence of sexy tutors!

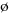 , φ, {}: Null or empty set
, φ, {}: Null or empty set


 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 





















13 Comments
曜
日
YES OF COURSE THEY EXIST!!!!!
I just never met any 🙁
曜
日
xD.. you are so funny...
I believe they exist too...and I want to find one...so I can learn calculus better 🙂
曜
日
can i ask how to do>.< nvm i juz do on my own wait fer ya to release de answer
曜
日
Peter: How do you confirm chop stamp know they exist when you haven't met any? Were you at Orchard Road the other day? 🙂
Mgccl: Which brings us to the next hypothesis: The Existence of Sexy Maths Tutors that CAN teach calculus well.
Kiroii: Surely you can easily do the first few parts of this question? As shown from past records, Miss Loi will only comment when someone has at least attempted the question here. Spoonfeeding is taboo in Jφss Sticks!
曜
日
what the! haha you rock man, can spin off a problem from this topic....
曜
日
Because I'm gullible, missloi... 🙂 You say you're a sexy maths 'cher, so I believe you. And, since you exist, you're real!
And, I've never MET you, remember?
曜
日
crazyhamster: Hamster rocks too. Especially your war report lol
Peter: In that case, don't be so gullible can? 😀
曜
日
Peter:
"since you exist"
how do you know Miss Loi really exist?
From "I think therefore I am"? then substitute I with Miss Loi?
"I think therefore I am" Logically equal to "I don't think therefore I am not"
I love math jokes...
anyway.. I tried to solve the question.. and here is what I got in 30 seconds, and I guess I'm wrong:
because
n(Y ∩ N) = k,
n(Y) = 7 x n(Y ∩ N),
n(N) = 4 x n(Y ∩ N),
n(ε) = 6 x n(Y’ ∩ N’)
suppose n(Y), n(N)
we have
n(Y) = 7k
n(N) = 4k
we know how many people didn't chose, 165
so we have
n(ε) = 165 * 6
and
n(ε) = 6* 165 = 990(yeeeah... ~~~)
n(Y ∪ N) = n(ε) - 165
= 825
now just have to find the value of k.
because we know. there exist a k in y and n, so subtract one from each of them.
we get
n(Y∩N') = 6k
n(N) = 4k
n(Y∩N') ∪ n(N) = n(Y ∪ N)
so 10k = 825
therefore
n(Y) = 825/10*7 = 577.5
because there is a decimal... so it don't seems like the right answer...
I failed!!! T.T
曜
日
Mgccl - don't read too much into my comments... missloi doesn't 🙂
曜
日
Mgccl,
You are brilliant! Not all O-Level students can jump straight to Part 2 and solve the whole question via making use of the 165 persons who didn't participate.
Though your answer is not quite right in the end, you're forgiven coz you probably didn't understand the term confirm chop stamp which means "100% sure" in our local context - which means you should exclude those hesitant ones who answered both Yes and No, hence you should be looking for:
n(Y∩N’) = (825/10)*6 = 495
BUT students will typically attempt part 1 before even taking a glance at part 2. So if you don't know about the 165 pax in part 2, do you think you'd still be able to fill up the four regions in Part 1?
曜
日
xD that's what I did wrong.
yeah.. it's still possible to fill up everything..
Miss Loi shall put up this diagram with the answers for easier reading and understanding:
n(Y∩N) = k Given
n(Y) = 7k = 7 x n(Y ∩ N) = 7k (Given)
n(Y∩N’) = n(Y) - n(Y∩N) = 6k Refer to the diagram if unsure
n(N) = 4k = 4 x n(Y ∩ N) = 4k (Given)
n(N∩Y’) = n(N) - n(Y∩N) = 3k Again refer to the diagram if unsure
Yes from what is given, students should not have any problems inserting the values in the first three regions. These are marks served on a platter.
n(ε) is tougher
n(ε) - n(Y’ ∩ N’) = n(Y∪N)
suppose n(Y’ ∩ N’) = x, we have
The only clue you're given with regards to the fourth region (i.e. n(Y’ ∩ N’)), is n(ε) = 6 x n(Y’ ∩ N’). So it's imperative that you recognize the first step is to let this 4th region be x!
6x - x = n(N∩Y’) + n(Y∩N’) + n(Y∩N)
⇒ entire region within the two circles = 6x - x = 5x
From your earlier workings, the region within the two circles is also equivalent to 6k+k+3k = 10k
⇒ 5x = 10k
... rest of workings are as straightforward as you've shown.
5x = 10 k
x = 2k
n(ε) = 12k
n(Y’ ∩ N’) = 2k (which is also equivalent to the 165 pax who didn't answer the survey!)
This is the part that left many stumped. Some (like you obviously) get it quickly while others can get stuck here a long time. That's why Miss Loi advise to move on (and revisit the last part of this question later when you have the time) if you're stuck. Afterall you should've already scored a decent amount of marks from the first portions of this question.
As for why k has a decimal point,
that's because Miss Loi had made a typo - she actually meant 166 paxlet's just assume that some of the people she surveyed were deemed too under-aged to discern the meaning of 'sexiness' - so these kids only count as half-persons 😉曜
日
Nice work Mgccl! Your workings are marked and some explanations added for the benefit of others.
BTW Miss Loi suspects you're a little over-aged for O-Level maths no?
曜
日
I don't know about it.. xD
I'm in US... so I don't take the O-Level math.