Home » Question of the Day » A-Maths Tuition Questions » Tora! Tora! Tora!

土
曜
日

2009

Sat

Aug

Tora! Tora! Tora!

(13)

Tuition given in the topic of A-Maths Tuition Questions from the desk of Miss Loi at 10:53 pm (Singapore time)

Updated on 10 September 2009

Miss Loi’s neglected car
click to see how horribly dirty it is

With the return of the haze and Miss Loi’s recent absence away in the Plane of Geometry, the poor car is looking a little neglected these days.

Dismayed and feeling depressed like a guilty parent each time she saw the dismal state of its paintwork, Miss Loi decided to send the car for a long-overdue wash plus pamper it with one of those much-touted “car grooming” sessions.

When she collected her car later in the day, her depression was cured instantly by the uplifting sight of its dazzling shine.

Words could not describe the silky sensation as she ran her slim fingers slowly across its smooth immaculately-waxed body, now free of the minuscule scratches and parabolic swirls that once scarred it.

It was almost like getting a new car, and this feeling stayed with her throughout her drive to a new student’s home, situated at the end of a straight road in a carpark-deprived area, for her next tuition session.

Bird’s eye view
– Miss Loi’s somewhere down there

As she slowly walked away, turning her head every few steps to admire the shine of her parked car, little did she realize that this glint of a shine would attract the attention of a little bird perched on a large tree at the end of the road.

Before long the area was slowly draped by a large shadow that caused Miss Loi to stop in her tracks, look up, and stare in utter horror at a huge fleet of birds flying towards her direction in an aggressive-looking formation, each with its … umm … “crosshairs” trained on the car.

The air raid siren in her mind sounded, and it was sheer luck that got her to the car in time before these terrors in the sky rained destruction upon the land.

When heroes are born

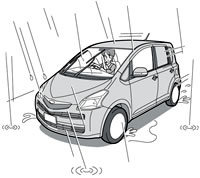
In heroic scenes that followed, left and right she swerved her car as she strived to save it from the relentless onslaught, narrowly avoiding bomb after bomb of waste matter that whistled through the air before landing with a sickening *splat* inches away from her.

Just when it seemed certain the car would be martyred on this very day, the flock began to turn back, as Miss Loi charged her way to freedom beyond the bombing range, immensely relieved that her superb driving skills had somehow saved her from the pounding.

But now she’s stuck at the end of the road, in a tense face-off with the evil birds on the tree at the opposite end readying themselves for the next bombing run, while her new student waits patiently for her in her house …

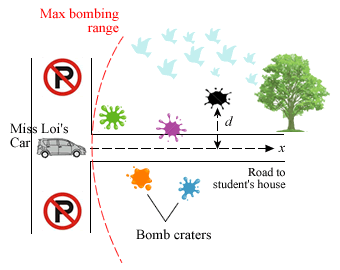
Noticing the pattern of the impact points along the road, Miss Loi suspects that their distance d from the centre of the road and the distance x along the road is connected by the equation 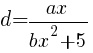$d={ax}/{bx^2+5}$

Bravely measuring a few samples along certain intervals on the road, Miss Loi recorded the following sets of values:

`x` (m)	5	10	15	20	25	30
`d` (m)	2.50	0.9	3.21	2.85	2.50	2.20

Given there’s nowhere else she can park her car other than along the centre of the narrow road (inside the bombing range), *use a suitable graph to examine the validity of Miss Loi’s equation, and estimate the values of a and b.

At which point (x) along the road should Miss Loi park her car to minimize the chances of it being hit i.e. where d is maximum?

*This is a Linear Law question requiring you to plot a graph on a piece of graph paper. You may generate a piece of graph paper online should you not to have one with you.

As Miss Loi doesn’t have any graph paper with her (shame on her!), can you please help her find the safest spot to park her shiny car so that she can start her new student’s tuition session on time with peace of mind?

頑張って!!!

Miss Loi

differentiation, linear law

Revision Exercise

To show that you have understood what Miss Loi just taught you from the centre, you must:

Comments & Reactions

Comments Feed

12 Comments

Kenny commented in tuition class
日
曜
日
2009
Aug
16
Sun
1:11am
1
May I suggest 3M DCF stickers? I hear it's absolutely wonderful against bird droppings.
- Link to this comment for your math/science tuition notes
Reply Kenny
mathslover commented in tuition class
日
曜
日
2009
Aug
16
Sun
6:52am
2
Maybe the next time you could recce the place before the actual first day and select n possible parking spaces where the probability of them all being taken is nearly 0.
Okay... mathslover is feeling lazy on a Sunday morning to find a mathematically sound solution. 😛
P.S. Its so difficult to make out exactly which part of the car is being captured... it looks like some UBO.
- Link to this comment for your math/science tuition notes
Reply mathslover
Capt. Chan commented in tuition class
日
曜
日
2009
Aug
16
Sun
12:46pm
3
Miss Loi,
I think the equation is valid and thevalues of a is 2.1 and the b value is... erm...I am not very sureT_T.
My workings are:
$d={ax}/{bx^2+5}$

Therefore, the gradient is -b and the Y-intercept is a. (The Linear Equation I got is Y=-bX+a, where Y is and X is dx.)
Based on the graph, I think you should park at d=10.
- Link to this comment for your math/science tuition notes
Reply Capt. Chan
Miss Loi Friend Miss Loi on Facebook @MissLoi commented in tuition class
月
曜
日
2009
Aug
17
Mon
7:44pm
4
Kenny: Are you talking about those black carbon fibre stickers for the car? A bit beng leh ...
mathlover: No time to check out the place beforehand - Miss Loi is a LMBFH tutor for this assignment 😉
And that UBO is actually the roof cum spoiler portion of the car, which Miss Loi thinks look more like a whaleshark now.
- Link to this comment for your math/science tuition notes
Reply Miss Loi
Miss Loi Friend Miss Loi on Facebook @MissLoi commented in tuition class
月
曜
日
2009
Aug
17
Mon
7:54pm
5
Ahhh nice to see you here Captain!
Unfortunately a isn't 2.1. For a start, can you list out your table of values and we'll take it from there? Miss Loi suspects that you may have been distracted while plotting your graph by a certain newbie bird that couldn't aim properly 😉
In such a typical 'experimental' type of Linear Law question that requires you to plot a graph, there can be more than one possible way to manipulate the original equation to form your Y = mX + c, ~~but please make sure that your Y and X contain only combinations of variables x and/or y that are independent of any constant!~~
~~*nudge nudge you to review your working above*~~
Scratch that. Following a ~~heated~~ discussion amongst The Order of The Temple this morning, we've concluded that Y and X may contain constants and coefficients (for e.g. 5y) so your workings and equations are fine.
Most likely the error arose somewhere from the way you've plotted your values and graph. Did your table and graph tally with the one Miss Loi plotted based on your equation?
- Link to this comment for your math/science tuition notes
Reply Miss Loi
Kenny commented in tuition class
火
曜
日
2009
Aug
18
Tue
8:46am
6
Beng yeah, but supposedly damn good if you get lots of droppings on your car. Spray some water and they are off.
- Link to this comment for your math/science tuition notes
Reply Kenny

Someone commented in tuition class

金
曜
日

2009

Aug

Fri

12:57am

$d=\frac{ax}{b{x^{2}}+5}$

Miss Loi: In most Linear Law questions that come with a table of values, and with life in general, the so-called tough and critical part usually lies at the beginning - where you try every little trick you've learnt in your Algebra, Logarithms, Indices etc. chapters to twist and turn (like a Rubik's Cube) in order to die die manipulate a given grotesque equation (usually with two unknowns) into its 'linear' form: Y = mX + c, where m and c must be free of all variables from the original equation.

In this example, since there isn't any unknown or variable in the powers of our equation e.g. a^x, x^b+1 etc. we can rule out the method of 'logging both sides' and instead proceed with using algebraic manipulation (i.e. cross-multiplying) to form our Y = mX + c expression, like what you've done ...

$()\times({b{x^{2}}+5})$
$d\times({b{x^{2}}+5})=ax$
$db{x^{2}}+5d=ax$
$\frac{()}{x^{2}}$
$db+\frac{5d}{x^{2}}=\frac{a}{x}$
$\frac{1}{d}\times()$
$b+\frac{5}{x^{2}}=\frac{a}{dx}$
$()\times\frac{1}{a}$
$(b+\frac{5}{x^{2}})\times\frac{1}{a}=\frac{1}{dx}$
${\frac{b}{a}}+{\frac{5}{a}}(\frac{1}{x^{2}})=\frac{1}{dx}$
$\frac{1}{dx}={\frac{5}{a}}(\frac{1}{x^{2}})+{\frac{b}{a}}$

$Y=mX+C$
$Y=\frac{1}{dx}$ , $m=\frac{5}{a}$ , $X=\frac{1}{x^{2}}$ , $C={\frac{b}{a}}$

Plot $\frac{1}{dx}$ against $\frac{1}{x^{2}}$

A little table and graph to aid the reader 😉

	0.0400	0.0100	0.0044	0.0025	0.0016	0.0011
	0.080	0.111	0.021	0.018	0.016	0.015

[Click Miss Loi's plotted masterpiece above to view it in its full glory]

Miss Loi's a little curious that you've selected as your X-axis since, as seen from the resultant graph, that inverse x² term is gonna lead to pretty small values of X that can be a little tricky to plot (and consequently slow you down during exam).

But in any case, all Linear Law students will pray for that magical moment when all that manipulating is finally validated, when they look up to the skies and thank the heavens upon seeing (most of) their constellation of plotted points for Y = mX + c align themselves on a straight line on the graph paper.

On the other hand, this moment may serve as a wake-up call for you to urgently re-examine your 'manipulation' workings if, to your horror, your 'constellation' resembles some random scatter diagram or the Crab Nebula.

All points other than (0.01, 0.111) lie on the line $y=1.666x+0.013$

So plotting against in this example, we find that 5 of the 6 points lie along a straight line (Rejoice!), with the 6th point (corresponding to x=10, y=0.9) being so far off the line that it belongs to a bird that obviously can't 'aim' well.

In such cases, your O-Level question will usually ask something like "It is suspected that an unusually large error occurs in one of the values of y. Identify the incorrect value and estimate its correct value."

For our question, it wasn't explicitly stated if the error, if indeed there's any, occurred in d or x and Miss Loi should have stated this in the question (sorry it's really been a busy week) to quell any big-time controversy of whether to leave out the 6th point entirely or draw a best-fit line through all 6 points.

But since it's pretty obvious that the 5 points lie almost perfectly on a straight line, we'll choose to ignore the 6th point since its abnormally-large distance from the line will affect the accuracy of estimating a and b if we choose to draw a best-fit line.

$\frac{5}{a}=1.666$
$\frac{1}{()}$
$\frac{a}{5}=\frac{1}{1.666}$
$\frac{a}{5}=\frac{500}{833}$
$()\times{5}$
$a=\frac{500}{833}\times{5}=\frac{2500}{833}\approx{3.00}$
${\frac{b}{a}}=0.013$
$()\times{a}$
$b=0.013\times{a}=0.013\times{\frac{2500}{833}}=\frac{65}{1666}\approx{0.0390}$

And so from your plotted graph above, we get the values of a and b as follows:

Gradient:
Y-intercept:

As an added note, Miss Loi has included within the graph some working to estimate the correct value of d if d is stated in the question to be erroneous (which we now know is at x = 10.

On the other hand, would it be possible to estimate from this graph the correct value of x if x is stated in the question to be erroneous (assuming d = 0.9 is correct)?

$d=\frac{ax}{b{x^{2}}+5}$
${\frac{d}{dx}}[d]$

Hope everyone remembers the a little Quotient Rule in Differentiation: $d/{dx}(u/v) = {v{du}/{dx} - u{dv}/{dx}}/{v^2}$ used here to differentiate our original equation i.e. $d={ax}/{bx^2+5}$ (now that a and b are known) to obtain the value of x when d is at its maximum.

$=\frac{(b{x^{2}}+5)(a)-(ax)(2bx)}{(b{x^{2}}+5)^{2}}$
$=\frac{ab{x^{2}}+5a-2ab{x^{2}}}{(b{x^{2}}+5)^{2}}$
$=\frac{5a-ab{x^{2}}}{(b{x^{2}}+5)^{2}}$
${\frac{d}{dx}}[d]=0$
$5a-ab{x^{2}}=0$
$a(5-b{x^{2}})=0$
$5-b{x^{2}}=0$
$()+b{x^{2}}=0$
$5=b{x^{2}}$
$\frac{()}{b}$
$\frac{5}{b}=x^{2}$
$\sqrt{()}$
$\sqrt{\frac{5}{b}}=x$
$x=\sqrt{\frac{5}{b}}=\sqrt{\frac{5}{\frac{65}{1666}}}\approx{11.3205056}\approx{11.3}$

Link to this comment for your math/science tuition notes

Reply Someone

Miss Loi Friend Miss Loi on Facebook @MissLoi commented in tuition class

月
曜
日

2009

Aug

Mon

10:18pm

It's worth noting that many Linear Law questions actually specify exactly the big Y and big X axes you're required to plot e.g. "... by plotting y against x² ..." to save you the trouble of having to 'manipulate' the original non-linear equation.

But for those who don't, Miss Loi (fresh from the satisfaction of seeing the car survive a week from the birds by parking at x ≈ 11.3 m) has adapted and compiled from an assessment book the following table of suggested Xs, Ys, m and c for a range of possible equations, which she hopes will help those of you who still have trouble forming your Y = mX+c:

Click to view

The above table is NOT for you to memorize! Please use it more as a guide for you to practice your 'manipulation' skills on a wide possible range of equations.

To emphasize that the above table is just a guide, it should be remembered that there can be more than one way to obtain your big Ys and Xs.

So just to illustrate this here's two more vastly-different graphs that Miss Loi has plotted for this same question, with the resultant similar estimated values for a and b:

Presenting Miss Loi's graph!

$x/d = (b/a){x^2} + 5/a doubleright Y = x/d, X = x^2$

	25	100	225	400	625	900
	2.000	11.111	4.673	7.018	10.000	13.636

Presenting Capt Chan's graph as derived from here!

	12.5	9	48.15	57	62.5	66
	2.500	0.450	1.070	0.713	0.500	0.367

Note that we cannot correct any possible error occurring in d or x in this graph. Do you know why? 😉

Once you've successfully performed your 'manipulation' (and avoid all the common careless mistakes like logarithm errors etc.), things get a little 'procedural' (read: STRAIGHT-FORWARD) in terms of plotting the graph and solving your unknowns via m and C and watch your marks go "1 Up" ... "1 Up" ... "1 Up" like in Mario Bros so do give yourself a chance a shot at the Linear Law question in the exam even if it looks a bit daunting!

Link to this comment for your math/science tuition notes

Reply Miss Loi

Someone commented in tuition class
月
曜
日
2009
Aug
24
Mon
10:51pm
9
I remember deriving another different equation, and the points did not lie on the line. There was a curve!
- Link to this comment for your math/science tuition notes
Reply Someone
Someone commented in tuition class
月
曜
日
2009
Aug
24
Mon
11:12pm
10
Oh... I realize I used the wrong chart type in Excel. :$
- Link to this comment for your math/science tuition notes
Reply Someone
Miss Loi Friend Miss Loi on Facebook @MissLoi commented in tuition class
火
曜
日
2009
Aug
25
Tue
4:40pm
11
You've committed a careless mistake when using Excel??? o.O
- Link to this comment for your math/science tuition notes
Reply Miss Loi
Someone commented in tuition class
火
曜
日
2009
Aug
25
Tue
7:32pm
12
For some reason, when I set the graph type to line, all the intervals are equally spaced, even though the differences between them are not. It only comes out fine when I set to x y scatter. Lol.
- Link to this comment for your math/science tuition notes
Reply Someone

YOUR CART

Tora! Tora! Tora!

Revision Exercise

12 Comments

Post a Comment

Latest News

About Miss Loi

Gratitudes

Peer Pressure

School Badges

Categories

Recent Posts

Jφss Sticks Most Popular

Archives